题目内容
在△ABC中, ,
,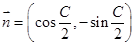 ,且
,且 的夹角是
的夹角是
(1)求角C;
(2)已知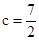 ,三角形ABC的面积
,三角形ABC的面积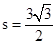 ,求a+b.
,求a+b.
(1) (2)
(2) .
.
解析试题分析:(1)由向量 的坐标根据向量模公式计算出
的坐标根据向量模公式计算出 =
= =1,由向量数量积坐标表示及二倍角的余弦公式可算出
=1,由向量数量积坐标表示及二倍角的余弦公式可算出 的数量积为
的数量积为 ,再由数量积的定义可得
,再由数量积的定义可得 的的数量积为
的的数量积为 ,从而得出
,从而得出 =
= ,即可求出角C;(2)由三角形面积公式及已知条件可求出
,即可求出角C;(2)由三角形面积公式及已知条件可求出 ,再由余弦定理和配凑法,可得到关于
,再由余弦定理和配凑法,可得到关于 的方程,再求出
的方程,再求出 .
.
试题解析:(1)由 ,
,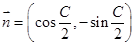 知,
知, =
= =1,
=1, =
= =
= ,
,
因为 的夹角是
的夹角是 ,所以
,所以 =
= =
= ,
,
所以 =
= ,又因为
,又因为 ,所以
,所以 =
= .
.
(2)由(1)知, =
= ,因为三角形ABC的面积
,因为三角形ABC的面积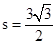 ,
,
所以 =
= =
= ,
,
所以 =6,
=6,
由余弦定理知, =
= =
= ,
,
解得 ,
,
所以 =
= .
.
考点:向量的数量积的定义及坐标表示;二倍角公式;三角形面积公式;余弦定理

练习册系列答案
相关题目
 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°. ,求PA;
,求PA;
 的内角
的内角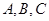 所对边的长分别是
所对边的长分别是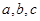 ,且
,且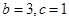 ,△
,△ ,求
,求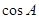 与
与 的值.
的值. 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小. 中,
中, ,
, ,
, .
.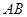 长;
长; 的值.
的值. ,并在点C测得塔顶A的仰角为
,并在点C测得塔顶A的仰角为 ,求塔高AB.
,求塔高AB.
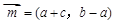 ,
,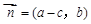 ,
,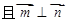 .
. ,求角A的值.
,求角A的值. 的内角
的内角 与
与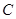 互补,
互补, .
. ;
;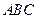 中,内角
中,内角 ,
,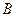 ,
, 对边的边长分别是
对边的边长分别是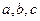 ,且
,且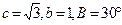 ,则△
,则△