题目内容
已知 的三内角
的三内角 、
、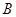 、
、 所对的边分别是
所对的边分别是 ,
, ,
, ,向量
,向量
 ,且
,且 。
。
(1)求角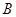 的大小;
的大小;
(2)若 ,求
,求 的范围。
的范围。
(1) (2)
(2)
解析试题分析:(1)由两向量的坐标,及两向量垂直,利用平面向量的数量积运算法则列出关系式,利用正弦定理化简,整理后利用两角和与差的正弦函数公式及诱导公式化简,求出 的值,即可确定出B的度数;
的值,即可确定出B的度数;
(2)由b及 的值,利用余弦定理列出关系式,再利用基本不等式求出
的值,利用余弦定理列出关系式,再利用基本不等式求出 的最大值,最后利用三角形两边之和大于第三边求出
的最大值,最后利用三角形两边之和大于第三边求出 的范围即可.
的范围即可.
(1) ,
, ,且
,且 ,
, ,
,
利用正弦定理化简得: ,整理得
,整理得 ,即
,即
又
(2) ,所以由余弦定理
,所以由余弦定理 ,即
,即 ,当且仅当
,当且仅当 时取等号,
时取等号, 即
即 ,又
,又

考点:正弦、余弦定理,基本不等式的运用

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 ,并在点C测得塔顶A的仰角为
,并在点C测得塔顶A的仰角为 ,求塔高AB.
,求塔高AB.
 的内角
的内角 所对的边分别为
所对的边分别为 .
. ;
; 的最小值.
的最小值. 的内角
的内角 与
与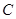 互补,
互补, .
. ;
; 、
、 、
、 分别为
分别为 的三边
的三边 、
、 、
、 所对的角,向量
所对的角,向量 ,
, ,且
,且 .
. ,求边
,求边 +
+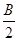 ),-1),且m⊥n.
),-1),且m⊥n. 中,已知
中,已知 ,
, ,试判断
,试判断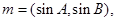
 ,且
,且 .
. ,求边c的长.
,求边c的长. 中,
中, 是角
是角 对应的边,向量
对应的边,向量 ,
, ,且
,且 .
. ;
; 的相邻两个极值的横坐标分别为
的相邻两个极值的横坐标分别为 、
、 ,求
,求 的单调递减区间.
的单调递减区间.