题目内容
在锐角 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 ,
, ,
, .
.
(1)求角 与边
与边 的值;
的值;
(2)求向量 在
在 方向上的投影.
方向上的投影.
(1)B= ,c=7;(2)
,c=7;(2) .
.
解析试题分析:(1)根据sin(B+C)的值,以及在△ABC中,A+B+C= ,可得
,可得 ,再由正弦定理可求得a,根据a,b以及cosA,根据余弦定理可以得到关于c的方程,从而得到c;(2)根据定义,
,再由正弦定理可求得a,根据a,b以及cosA,根据余弦定理可以得到关于c的方程,从而得到c;(2)根据定义, 在
在 方向上的投影为
方向上的投影为 ,再代入(1)中的数据即可.
,再代入(1)中的数据即可.
(1)由 , (2分)
, (2分)
由正弦定理,有 ,所以
,所以 =
= . (4分)
. (4分)
由题知 ,故
,故 . (5分)
. (5分)
又 ,根据余弦定理,
,根据余弦定理, ,解得
,解得 . (8分);
. (8分);
(2)由(1)知, ,向量
,向量 在
在 方向上的投影为|
方向上的投影为| |
| =
= . (12分).
. (12分).
考点:1、正弦定理与余弦定理;2、平面向量数量积.

练习册系列答案
相关题目
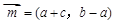 ,
,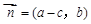 ,
,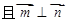 .
. ,求角A的值.
,求角A的值. 的内角
的内角 与
与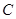 互补,
互补, .
. ;
; +
+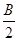 ),-1),且m⊥n.
),-1),且m⊥n. 中,已知
中,已知 ,
, ,试判断
,试判断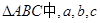 分别是角A、B、C的对边,
分别是角A、B、C的对边,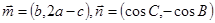 ,且
,且 .
.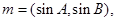
 ,且
,且 .
. ,求边c的长.
,求边c的长. 中,角
中,角 所对的边分别为
所对的边分别为 ,且
,且 成等差数列.
成等差数列. 的大小;
的大小; ,求
,求 边上中线长的最小值.
边上中线长的最小值. bc.
bc.