题目内容
20.曲线y=xex+1在点(1,1)处切线的斜率等于( )| A. | 2e | B. | 2e2 | C. | 2 | D. | 1 |
分析 求函数的导数,利用导数的几何意义即可求出对应的切线斜率.
解答 解:函数的导数为f′(x)=ex+1+xex+1=(1+x)ex+1,
当x=1时,f′(1)=2e2,
即曲线y=xex-1在点(1,1)处切线的斜率k=f′(1)=2e2,
故选:B.
点评 本题主要考查导数的几何意义,正确求函数的导数是解决本题的关键,比较基础.

练习册系列答案
相关题目
11.已知角α的始边为x轴的正半轴,点(1,3)是角α终边上的一点,则tanα=( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
15.如图所示,在△ABC中,点D、E、F分别是边AB、BC、AC的中点,则下面结论正确的是( )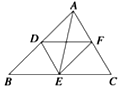

| A. | $\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{FA}$ | B. | $\overrightarrow{DE}+\overrightarrow{AF}=0$ | C. | $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}≠0$ | D. | $\overrightarrow{DE}-\overrightarrow{DF}=\overrightarrow{AD}$ |
10.如图,在平面四边形ABCD中,AD=1,CD=2,AC=$\sqrt{7}$.cos∠BAD=-$\frac{\sqrt{7}}{14}$,sin∠CBA=$\frac{\sqrt{21}}{6}$,则BC的长为( )
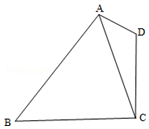

| A. | $\sqrt{7}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{7}$ |
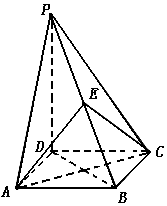 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上.