如图所示.在△ABC中.点D.E.F分别是边AB.BC.AC的中点.则下面结论正确的是( )A．$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{FA}$B．$\overrightarrow{DE}+\overrightarrow{AF}=0$C．$\overrightarrow{AB}+\overrightarrow{BC}+\ov 题目和参考答案——青夏教育精英家教网—

题目内容

15．如图所示，在△ABC中，点D、E、F分别是边AB、BC、AC的中点，则下面结论正确的是（　　）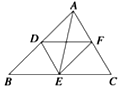

A．

$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{FA}$

B．

$\overrightarrow{DE}+\overrightarrow{AF}=0$

C．

$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}≠0$

D．

$\overrightarrow{DE}-\overrightarrow{DF}=\overrightarrow{AD}$

分析根据平面向量的线性运算法则与共线定理，对选项中的命题进行分析、判断正误即可．

解答解：△ABC中，点D、E、F分别是边AB、BC、AC的中点，
∴$\overrightarrow{AE}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）=$\overrightarrow{AD}$+$\overrightarrow{AF}$，∴A错误；
$\overrightarrow{DE}$+$\overrightarrow{AF}$=2$\overrightarrow{DE}$≠$\overrightarrow{0}$，∴B错误；
$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CA}$=$\overrightarrow{AC}$+$\overrightarrow{CA}$=$\overrightarrow{0}$，∴C错误；
$\overrightarrow{DE}$-$\overrightarrow{DF}$=$\overrightarrow{FE}$=$\overrightarrow{AD}$，∴D正确．
故选：D．

点评本题考查了平面向量的线性运算法则与共线定理的应用问题，是基础题．

练习册系列答案

6．在△ABC中，角A，B，C的对边分别为a，b，c，且满足$cos\frac{A}{2}=\frac{{2\sqrt{5}}}{5}，\overrightarrow{AB}•\overrightarrow{AC}=15$．
（1）求△ABC的面积；
（2）若tanB=2，求a的值．

3．已知角θ的终边在射线y=2x（x≥0）上．
（1）求tanθ的值；
（2）求$\frac{2cosθ+3sinθ}{cosθ-3sinθ}+sinθcosθ$的值．

10．函数f（x）=lnx-x的单调增区间为（　　）

20．曲线y=xe^x+1在点（1，1）处切线的斜率等于（　　）

2e²

7．求：$\frac{{sin330°•tan（-\frac{13}{3}π）}}{{cos（-\frac{19}{6}π）•cos690°}}$的值．

4．P为椭圆$\frac{x^2}{{2{b^2}}}+\frac{y^2}{b^2}=1（{b＞0}）$上异于左右顶点A₁、A₂的任意一点，则直线PA₁与PA₂的斜率之积为定值$-\frac{1}{2}$．将这个结论类比到双曲线，得出的结论为：P为双曲线$\frac{x^2}{{2{b^2}}}-\frac{y^2}{b^2}=1（{b＞0}）$上异于左右顶点A₁、A₂的任意一点，则（　　）

	A．	直线PA₁与PA₂的斜率之和为定值$\frac{1}{2}$		B．	直线PA₁与PA₂的斜率之和为定值2
	C．	直线PA₁与PA₂的斜率之积为定值$\frac{1}{2}$		D．	直线PA₁与PA₂的斜率之积为定值2

5．若关于x不等式xlnx-x³+x²≤ae^x恒成立，则实数a的取值范围是（　　）

试题分类