题目内容
已知三个正数a,b,c成等比数列,但不成等差数列.求证:
,
,
不成等差数列.
| a |
| b |
| c |
考点:等比数列的性质,等差关系的确定
专题:证明题,等差数列与等比数列
分析:假设
,
,
成等差数列,则2
=
+
,结合题意可得b=
,代入上式可得a=b=c,与已知矛盾.
| a |
| b |
| c |
| b |
| a |
| c |
| ac |
解答:
证明:假设
,
,
成等差数列,则2
=
+
,即4b=a+c+2
①,
因为a,b,c成等比数列,故b2=ac,即b=
②
由①②得a=c,
∴a=b=c
与a,b,c不成等差数列矛盾
故
,
,
不成等差数列.
| a |
| b |
| c |
| b |
| a |
| c |
| ac |
因为a,b,c成等比数列,故b2=ac,即b=
| ac |
由①②得a=c,
∴a=b=c
与a,b,c不成等差数列矛盾
故
| a |
| b |
| c |
点评:通过用利用反证法证明
,
,
不成等差数列,体会等差数列与等比数列的性质.
| a |
| b |
| c |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
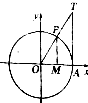
已知MP、OM、AT分别是60°角的正弦线、余弦线、正切线,如图,则一定有( )

| A、MP<OM<AT |
| B、AT<OM<MP |
| C、OM<MP<AT |
| D、OM<AT<MP |
下表为某大型超市一个月的销售收入情况表,则本月销售收入的平均增长率( )
| 日期 | 5 | 10 | 15 | 20 | 25 | 30 |
| 销售收入(万元) | 20 | 40 | 90 | 160 | 275 | 437.5 |
| A、一样 | B、越来越大 |
| C、越来越小 | D、无法确定 |
一个几何体的三视图如图所示,则该几何体的正视图面积为( )


| A、2+3π | ||
B、2+
| ||
C、4+
| ||
| D、4+π |