题目内容
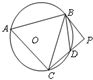 如图,PB为△ABC外接圆O的切线,BD平分∠PBC,交圆O于D,C,D,P共线.若AB⊥BD,PC⊥PB,PD=1,则圆O的半径是
如图,PB为△ABC外接圆O的切线,BD平分∠PBC,交圆O于D,C,D,P共线.若AB⊥BD,PC⊥PB,PD=1,则圆O的半径是考点:与圆有关的比例线段
专题:立体几何
分析:连结AD,由PB为圆O的切线,得∠PBD=∠BCP=∠BAD,结合BD为∠PBC的平分线,可得∠PDB=2∠PBD=60°,在Rt△BPD中,由PD=1,得BD=2,由Rt△ABD与Rt△BPD的内角关系得AD的长度,即得圆O的半径.
解答:
解:如右图所示,连结AD,∵PB为圆O的切线,∴∠PBD=∠BCD=∠BAD,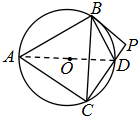
∵BD为∠PBC的平分线,∴∠PBD=∠CBD,
∴∠PDB=∠CBD+∠BCD=∠PBD+∠PBD=2∠PBD,
又∵PC⊥PB,∴∠PBD=∠BCD=∠CBD=∠BAD=30°,∠PDB=60°.
由PD=1,得BD=2PD=2.
在△ABD中,∵AB⊥BD,∴AD是圆O的直径,且直径AD=2BD=4,
∴圆O的半径为2.
故答案为:2.

∵BD为∠PBC的平分线,∴∠PBD=∠CBD,
∴∠PDB=∠CBD+∠BCD=∠PBD+∠PBD=2∠PBD,
又∵PC⊥PB,∴∠PBD=∠BCD=∠CBD=∠BAD=30°,∠PDB=60°.
由PD=1,得BD=2PD=2.
在△ABD中,∵AB⊥BD,∴AD是圆O的直径,且直径AD=2BD=4,
∴圆O的半径为2.
故答案为:2.
点评:本题考查了圆的弦切角定理及直角三角形的有关性质等,解题的突破口是得到∠BDP与∠PBD的2倍关系.应记住一些常用的结论,如
(1)弦切角等于它夹的弧所对的圆周角.
(2)在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半;如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.
(3)同弧(或等弧)所对的圆周角相等.
(4)90°的圆周角所对的弦是直径,直径所对的圆周角是90°.
(1)弦切角等于它夹的弧所对的圆周角.
(2)在直角三角形中,如果有一个锐角等于30°,那么它所对的直角边等于斜边的一半;如果有一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.
(3)同弧(或等弧)所对的圆周角相等.
(4)90°的圆周角所对的弦是直径,直径所对的圆周角是90°.

练习册系列答案
相关题目
命题“?x∈R,x2+2x+2≤0”的否定是( )
| A、?x∈R,x2+2x+2>0 |
| B、?x∈R,x2+2x+2≤0 |
| C、?x∈R,x2+2x+2>0 |
| D、?x∈R,x2+2x+2≥0 |
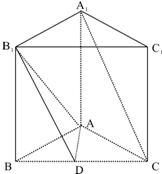 如图,底面是正三角形的直三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=2.
如图,底面是正三角形的直三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=2.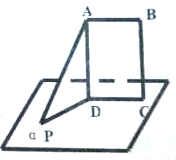 如图,已知AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.
如图,已知AB∥α,AD⊥α,BC⊥α,垂足为D、C,PA⊥AB,求证:CD⊥平面PAD.