题目内容
13．f（x）是周期为4的奇函数．且f（-1）=2，求f（13）．分析 根据周期性奇函数定义得出f（13）=f（1）=-f（-1）=-2，即可求解答案．
解答 解：∵f（x）是周期为4的奇函数．且f（-1）=2，
∴f（13）=f（1）=-f（-1）=-2，
故答案为-2．
点评 本题考查了函数的性质，运奇函数的定义，周期性求解函数值，难度很小，属于容易题．
练习册系列答案
相关题目
1．已知点M在角θ终边的延长线上，且|OM|=2，则M的坐标为（ ）
| A． | （2cosθ，2sinθ） | B． | （-2cosθ，2sinθ） | C． | （-2cosθ，-2sinθ） | D． | （2cosθ，-2sinθ） |
8．在△ABC中，若sinA：sinB：sinC=2：3：4，则最大角的余弦值为（ ）
| A． | $\frac{1}{3}$ | B． | $-\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $-\frac{1}{4}$ |
18．若tan（α+80°）=4sin420°，则tan（α+20°）的值为（ ）
| A． | -$\frac{\sqrt{3}}{5}$ | B． | $\frac{3\sqrt{3}}{5}$ | C． | $\frac{\sqrt{3}}{19}$ | D． | $\frac{\sqrt{3}}{7}$ |
5．
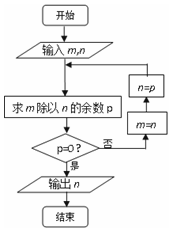执行右面的程序框图，如果输入m=72，n=30，则输出的n是（ ）
执行右面的程序框图，如果输入m=72，n=30，则输出的n是（ ）| A． | 12 | B． | 6 | C． | 3 | D． | 0 |
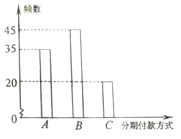某知名品牌汽车深受消费者喜爱，但价格昂贵．某汽车经销商推出A、B、C三种分期付款方式销售该品牌汽车，并对近期100位采用上述分期付款的客户进行统计分析，得到如下的柱状图．已知从A、B、C三种分期付款销售中，该经销商每销售此品牌汽车1俩所获得的利润分别是1万元，2万元，3万元．现甲乙两人从该汽车经销商处，采用上述分期付款方式各购买此品牌汽车一辆．以这100位客户所采用的分期付款方式的频率代替1位客户采用相应分期付款方式的概率．