题目内容
椭圆C的中点在原点,焦点在x轴上,若椭圆C的离心率等于
,且它的一个顶点恰好是抛物线x2=8
y的焦点,则椭圆C的标准方程为 .
| 1 |
| 2 |
| 3 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由题意设椭圆C的标准方程为
+
=1,a>b>0,由已知得
,由此能求出椭圆C的标准方程.故答案为:
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
|
| x2 |
| 16 |
| y2 |
| 12 |
解答:
解:由题意设椭圆C的标准方程为
+
=1,a>b>0,
∵抛物线x2=8
y的焦点为F(0,2
),
∴由已知得
,解得a=4,b=2
,
∴椭圆C的标准方程为
+
=1.
故答案为:
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
∵抛物线x2=8
| 3 |
| 3 |
∴由已知得
|
| 3 |
∴椭圆C的标准方程为
| x2 |
| 16 |
| y2 |
| 12 |
故答案为:
| x2 |
| 16 |
| y2 |
| 12 |
点评:本题考查椭圆标准方程的求法,是基础题,解题时要注意椭圆的简单性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

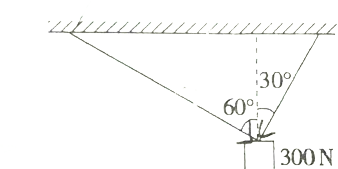 如图所示,在重300N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°,60°,当整个系统处于平衡状态时,求两根绳子的拉力.
如图所示,在重300N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°,60°,当整个系统处于平衡状态时,求两根绳子的拉力.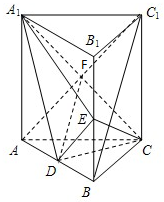 如图,直三棱柱ABC-A1B1C1中,D、E分别为AB、BB1的中点.
如图,直三棱柱ABC-A1B1C1中,D、E分别为AB、BB1的中点.