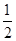题目内容
已知数列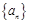 是首项为1,公差为
是首项为1,公差为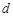 的等差数列,数列
的等差数列,数列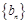 是首项为1,公比为
是首项为1,公比为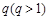 的等比
的等比
数列.
(1)若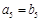 ,
,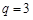 ,求数列
,求数列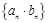 的前
的前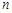 项和;
项和;
(2)若存在正整数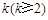 ,使得
,使得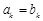 .试比较
.试比较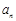 与
与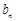 的大小,并说明理由.
的大小,并说明理由.
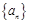 是首项为1,公差为
是首项为1,公差为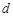 的等差数列,数列
的等差数列,数列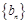 是首项为1,公比为
是首项为1,公比为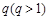 的等比
的等比数列.
(1)若
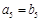 ,
,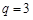 ,求数列
,求数列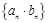 的前
的前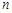 项和;
项和;(2)若存在正整数
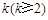 ,使得
,使得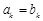 .试比较
.试比较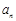 与
与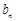 的大小,并说明理由.
的大小,并说明理由.(1)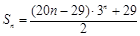 ;(2) 当
;(2) 当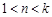 时,
时,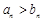 ;当
;当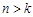 时,
时,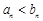 ;当
;当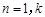 时,
时,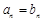 .
.
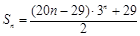 ;(2) 当
;(2) 当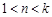 时,
时,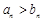 ;当
;当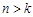 时,
时,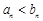 ;当
;当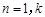 时,
时,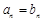 .
.试题分析:(1)利用基本量思想求解两个数列的通项公式,然后才有错位相减法求解数列
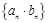 的前
的前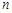 项和;(2)利用
项和;(2)利用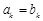 等量关系关系,减少公差d,进而将
等量关系关系,减少公差d,进而将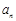 与
与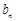 进行表示,然后才有作差比较进行分析,注意分类讨论思想的应用.
进行表示,然后才有作差比较进行分析,注意分类讨论思想的应用.试题解析:(1)依题意,
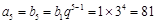 ,
,故
 ,
,所以
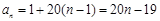 , 3分
, 3分令
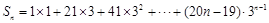 , ①
, ①则
 , ②
, ②①
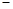 ②得,
②得,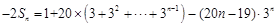 ,
,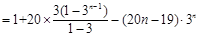
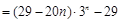 ,
,所以
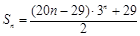 . 7分
. 7分(2)因为
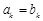 ,
,所以
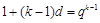 ,即
,即 ,
,故
 ,
,又
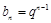 , 9分
, 9分所以
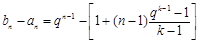
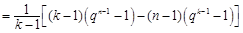
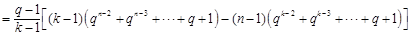
11分
(ⅰ)当
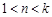 时,由
时,由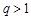 知
知
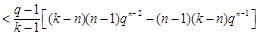
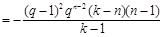
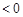 , 13分
, 13分(ⅱ)当
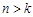 时,由
时,由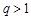 知
知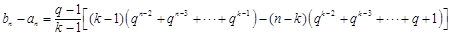
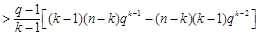
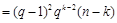
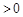 ,
,综上所述,当
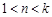 时,
时,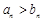 ;当
;当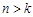 时,
时,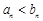 ;当
;当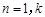 时,
时,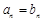 . 16分
. 16分(注:仅给出“
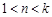 时,
时,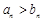 ;
;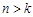 时,
时,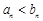 ”得2分.)
”得2分.)方法二:(注意到数列的函数特征,运用函数性质求解)
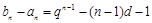 (易知
(易知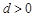 ),
),令
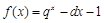 ,有
,有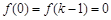 ,
,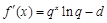 ,
,令
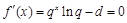 ,则
,则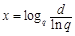 .记
.记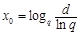 .
.若
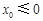 ,则在
,则在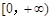 上
上 ,函数
,函数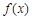 在
在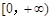 上为单调增函数,则
上为单调增函数,则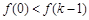 ,
,这与
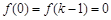 相矛盾;
相矛盾;若
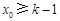 ,则在
,则在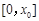 上
上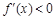 ,函数
,函数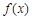 在
在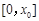 上为单调减函数,则
上为单调减函数,则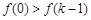 ,
,这与
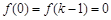 相矛盾;
相矛盾;所以,
 .
.故在
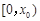 上
上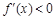 ,函数
,函数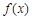 在
在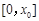 上为单调减函数,
上为单调减函数,在
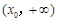 上
上 ,函数
,函数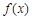 在
在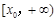 上为单调增函数.
上为单调增函数.因为
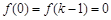 ,所以,当
,所以,当 时,
时,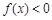 ,当
,当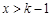 时,
时,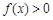 ,
,所以,当
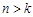 时,
时,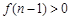 ,即
,即 ,
,当
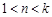 时,
时,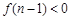 ,即
,即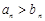 ,
,综上所述,当
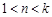 时,
时,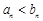 ;当
;当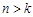 时,
时,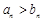 ;当
;当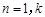 时,
时,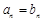 .
.
练习册系列答案
相关题目
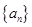 的前
的前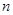 项和为
项和为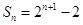 ,数列
,数列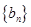 是首项为
是首项为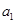 ,公差为
,公差为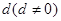 的等差数列,且
的等差数列,且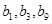 成等比数列.
成等比数列.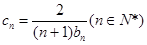 ,求数列
,求数列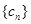 的前
的前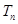 .
.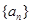 的首项
的首项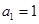 ,公差
,公差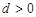 .且
.且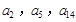 分别是等比数列
分别是等比数列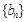 的
的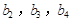 .
. 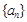 与
与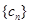 对任意自然数
对任意自然数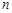 均有
均有
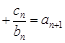 成立,求
成立,求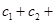
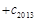 的值.
的值.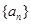 中,
中,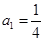 ,
,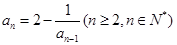 ,若数列
,若数列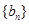 满足
满足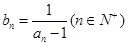 .
.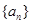 的前
的前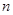 项和为
项和为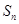 ,且
,且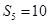 ,
,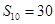 ,则
,则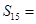 ( )
( )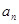 },满足
},满足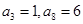 ,则此数列的前
,则此数列的前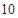 项的和
项的和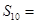 .
.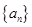 的前n项和为
的前n项和为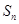 ,若
,若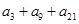 的值为常数,则下列各数中也是常数的是( ).
的值为常数,则下列各数中也是常数的是( ). 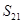
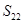

 S
S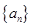 是递增数列,
是递增数列,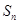 是
是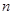 项和。若
项和。若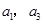 是方程
是方程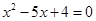 的两个根,则
的两个根,则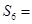 .
.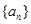 为等差数列,且
为等差数列,且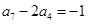 ,
,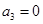 ,则公差
,则公差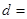 ( )
( )