题目内容
4．在空间直角坐标系中，已知点A（1，0，1），B（-1，1，2），则线段AB的长度为$\sqrt{6}$．分析 根据两点间的距离公式，进行计算即可．
解答 解：空间直角坐标系中，点A（1，0，1），B（-1，1，2），
所以线段AB的长度为|AB|=$\sqrt{{（-1-1）}^{2}{+（1-0）}^{2}{+（2-1）}^{2}}$=$\sqrt{6}$．
故答案为：$\sqrt{6}$．
点评 本题考查了空间直角坐标系中两点间的距离公式的应用问题，是基础题目．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
15．
如图，四棱锥P-ABCD中，ABCD是正方形，侧棱PA⊥底面ABCD，PA=AB，M、N分别是PC、PD的中点，则异面直线BM与CN所成的角大小为（ ）
如图，四棱锥P-ABCD中，ABCD是正方形，侧棱PA⊥底面ABCD，PA=AB，M、N分别是PC、PD的中点，则异面直线BM与CN所成的角大小为（ ）| A． | $\frac{π}{2}$ | B． | $\frac{π}{3}$ | C． | arccos$\frac{\sqrt{2}}{3}$ | D． | π-arccos$\frac{\sqrt{2}}{3}$ |
19．已知函数f（x）=$\left\{\begin{array}{l}{kx+1，}&{x≤0}\\{lnx，}&{x＞0}\end{array}\right.$，则方程f（f（x））+2=0有4个不同的实数解的充要条件是（ ）
| A． | k＜0 | B． | k＞0 | C． | -1＜k＜1 | D． | -1≤k≤1 |
9．已知命题p：cosα≠0是α≠2kπ（k∈Z）的充分必要条件，
命题q：设随机变量ζ～N（0，1），若P（ξ≥$\frac{3}{2}$）=m，则P（-$\frac{3}{2}$＜ξ＜0）=$\frac{1}{2}$-m，
下列命题是假命题的为（ ）
命题q：设随机变量ζ～N（0，1），若P（ξ≥$\frac{3}{2}$）=m，则P（-$\frac{3}{2}$＜ξ＜0）=$\frac{1}{2}$-m，
下列命题是假命题的为（ ）
| A． | p∧q | B． | p∨q | C． | ￢p∧q | D． | ￢p∨q |
16．已知向量$\overrightarrow{a}$=（-3cosα，2）与向量$\overrightarrow{b}$=（3，-4sinα）平行，则锐角α等于（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{5π}{12}$ |
13．在如图的正方体中，M、N分别为棱BC和棱CC′的中点，则异面直线B′D′和MN所成的角为（ ）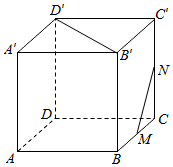
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |