题目内容
12.在△ABC中,角A,B,C的对边分别为a,b,c,已知acosB-(2c-b)cosA=0.(Ⅰ)求角A的大小;
(Ⅱ)若a=4,求△ABC面积的最大值.
分析 (Ⅰ)已知等式利用正弦定理化简,整理后求出cosA的值,即可确定出角A的大小;
(Ⅱ)由a,cosA的值,利用余弦定理列出关系式,再利用基本不等式求出bc的最大值,即可确定出三角形ABC面积的最大值.
解答 解:(Ⅰ)在△ABC中,已知等式acosB-(2c-b)cosA=0,
利用正弦定理化简得:sinAcosB-(2sinC-sinB)cosA=0,
整理得:sinAcosB+sinBcosA=2sinCcosA,即sin(A+B)=sinC=2sinCcosA,
∴cosA=$\frac{1}{2}$,
∵A为三角形内角,
∴A=$\frac{π}{3}$;
(Ⅱ)∵a=4,A=$\frac{π}{3}$,
∴由余弦定理得:16=b2+c2-bc≥2bc-bc=bc,即bc≤16,
当且仅当b=c时取等号,
∴S△ABC=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc≤4$\sqrt{3}$,当且仅当b=c时取等号,
则△ABC面积的最小值为4$\sqrt{3}$.
点评 此题考查了正弦、余弦定理,三角形面积公式,以及两角和与差的正弦函数公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
17. 某学校为了宣传环保知识,举办了“环保知识竞赛”活动
某学校为了宣传环保知识,举办了“环保知识竞赛”活动
(1)若从全校高一至高三的学生答卷中抽取了100份,成绩统计结果如表所示,分别求出n,a,b的值;
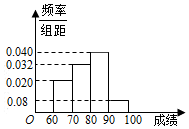
(2)若对高一年级1000名学生的成绩进行统计,结果为如图频率分布直方图;若成绩在90分以上的同学授予“环保之星”,从成绩在[60,70]和(90,100]的同学中按分层抽样的方法选出7人,求从这7人中随机抽取2人,恰有1人是“环保之星”的概率.
 某学校为了宣传环保知识,举办了“环保知识竞赛”活动
某学校为了宣传环保知识,举办了“环保知识竞赛”活动(1)若从全校高一至高三的学生答卷中抽取了100份,成绩统计结果如表所示,分别求出n,a,b的值;
| 年级 | 抽取份数 | 优秀人数 | 优秀率 |
| 高一 | 40 | a | 0.5 |
| 高二 | n | 18 | 0.6 |
| 高三 | 30 | 21 | b |
1.设全集为R,集合M={x|x2>1},N={x∈Z||x|≤2},则(∁RM)∩N=( )
| A. | {0} | B. | {2} | C. | {-1,0,1} | D. | {-2,0,2} |