题目内容
9.已知命题p:cosα≠0是α≠2kπ(k∈Z)的充分必要条件,命题q:设随机变量ζ~N(0,1),若P(ξ≥$\frac{3}{2}$)=m,则P(-$\frac{3}{2}$<ξ<0)=$\frac{1}{2}$-m,
下列命题是假命题的为( )
| A. | p∧q | B. | p∨q | C. | ¬p∧q | D. | ¬p∨q |
分析 根据充分条件和必要条件的定义以及正态分布的概率关系分别判断两个命题的真假结合复合命题之间的关系进行判断即可.
解答 解:若cosα≠0则α≠kπ+$\frac{π}{2}$,则α≠2kπ不成立,反之若α=kπ+$\frac{π}{2}$满足α≠2kπ,但cosα=0,故cosα≠0是α≠2kπ(k∈Z)的既不充分也不必要条件,故p是假命题,
若随机变量ζ~N(0,1),则函数关于x=0对称,
若P(ξ≥$\frac{3}{2}$)=m,则P(ξ≥$\frac{3}{2}$)=P(ξ≤-$\frac{3}{2}$)=m,
则P(-$\frac{3}{2}$<ξ<0)=$\frac{1}{2}$[1-P(ξ≥$\frac{3}{2}$)-P(ξ≤-$\frac{3}{2}$)=$\frac{1}{2}$(1-2m)=$\frac{1}{2}$-m,故q是真命题,
则p∧q是假命题,p∨q,¬p∧q,¬p∨q都是真命题,
故选:A.
点评 本题主要考查命题的真假判断,涉及充分条件和必要条件,正态分布的概率计算以及复合命题之间的关系,比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17. 某学校为了宣传环保知识,举办了“环保知识竞赛”活动
某学校为了宣传环保知识,举办了“环保知识竞赛”活动
(1)若从全校高一至高三的学生答卷中抽取了100份,成绩统计结果如表所示,分别求出n,a,b的值;
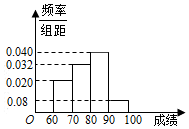
(2)若对高一年级1000名学生的成绩进行统计,结果为如图频率分布直方图;若成绩在90分以上的同学授予“环保之星”,从成绩在[60,70]和(90,100]的同学中按分层抽样的方法选出7人,求从这7人中随机抽取2人,恰有1人是“环保之星”的概率.
 某学校为了宣传环保知识,举办了“环保知识竞赛”活动
某学校为了宣传环保知识,举办了“环保知识竞赛”活动(1)若从全校高一至高三的学生答卷中抽取了100份,成绩统计结果如表所示,分别求出n,a,b的值;
| 年级 | 抽取份数 | 优秀人数 | 优秀率 |
| 高一 | 40 | a | 0.5 |
| 高二 | n | 18 | 0.6 |
| 高三 | 30 | 21 | b |
1.设全集为R,集合M={x|x2>1},N={x∈Z||x|≤2},则(∁RM)∩N=( )
| A. | {0} | B. | {2} | C. | {-1,0,1} | D. | {-2,0,2} |
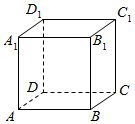 (普通中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).问质点从A点出发又回到起点A走完的段数是( )
(普通中学做)ABCD-A1B1C1D1是棱长为1的正方体,一个质点从A出发沿正方体的面对角线运动,每走完一条面对角线称为“走完一段”,质点的运动规则如下:运动第i段与第i+2所在直线必须是异面直线(其中i是正整数).问质点从A点出发又回到起点A走完的段数是( )