题目内容

已知函数f（x）=2tan（kx-
π
3
）的最小正周期T满足1＜T＜
3
2
，求正整数k的值，并指出f（x）的奇偶性、单调区间．
考点：三角函数的周期性及其求法,正切函数的单调性,正切函数的奇偶性与对称性
专题：三角函数的图像与性质
分析：由 1＜
π
k
＜
3
2
，求得k的范围，可得正整数k的值，可得f（x）=2tan（3x-
π
3
）．根据函数f（x）的定义域不关于原点对称，可得f（x）是非奇非偶函数．令nπ-
π
2
＜3x-
π
3
＜nπ+
π
2
，n∈z，求得x的范围，可得f（x）的增区间．
解答： 解：由题意可得 1＜
π
k
＜
3
2
，求得
2π
3
＜k＜π，故正整数k的值为3，故f（x）=2tan（3x-
π
3
）．
由3x-
π
3
≠nπ+
π
2
，n∈z，可得x≠
nπ
3
+
5π
18
，n∈z，故函数f（x）的定义域不关于原点对称，
故f（x）是非奇非偶函数．
令nπ-
π
2
＜3x-
π
3
＜nπ+
π
2
，n∈z，求得
nπ
3
-
π
18
＜x＜nπ+
5π
18
，n∈z，
故函数f（x）的单调增区间为（得
nπ
3
-
π
18
，nπ+
5π
18
 ），n∈z．
点评：本题主要考查正切函数的周期性、奇偶性和单调性，属于基础题．
练习册系列答案
相关题目
已知命题：p：在△ABC中，sinA＞sinB的充分不必要条件是A＞B；q：?x∈R，x2+2x+2≤0．则下列命题为真命题的是（　　）
A、p∧qB、￢p∧q
C、￢p∨qD、p∨q
已知集合A={y|y=ax2+3x+1，a∈R，x∈R}，B={x|y=
3-x
+2x+1，x∈R}，若B⊆A，则a的取值范围
 
．
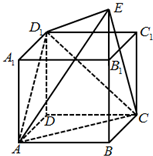如图长方体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形，|BB1|=a，E为BB1延长线上的一点且满足|BB1|•|B1E|=1．
（1）求证：D1E⊥平面AD1C；
（2）当a=1时，求二面角E-AC-D1的平面角的余弦值．
已知函数f（x）=
x+2
+k，k为已知的实数，
（1）求函数f（x）的值域；并判断其在定义域上的单调性（不必证明）；
（2）当k=-2时，设f（x）≤0的解集为A，函数g（x）=lg（sin2
π
6
x-3sin
π
6
x•cos
π
6
x+acos2
π
6
x）的定义域为B，若（A∪B）⊆B，求实数a的取值范围．
（3）若存在实数a，b≥-2且a＜b，使f（x）在[a，b]上的值域为[2a，2b]，求实数k的取值范围．
抛物线y=2x2-1的顶点为A，其上一动点P（x1，y1），则线段PA的中点M的轨迹方程是
 
．
若函数g（x）=ax-x-a（a＞0且a≠1）图象上有两个不同的点关于原点对称，则a的取值范围是
 
．
已知椭圆
x2
4
+y2=1与直线x-y+b=0相交于P、Q两点，O为坐标原点，若OP⊥OQ，求b的值．
设M是椭圆
x2
25
+
y2
16
=1上的一点，F1，F2为焦点，∠F1MF2=
π
6
，则△MF1F2的面积为（　　）
A、
16
3
3
B、16(2+
3
)
C、16(2-
3
)
D、16

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网