题目内容
12.在直三棱柱ABC-A1B1C1中,BC⊥AC,AC=12,BC=5,若一个球和它的各个面都相切,则该三棱柱的表面积为( )| A. | 60 | B. | 180 | C. | 240 | D. | 360 |
分析 棱柱底面三角形的内切圆即为球的大圆,棱柱的高为球的直径.
解答 解:∵AC=12,BC=5,BC⊥AC,∴AB=13.
设棱柱的内切球的半径为r,则Rt△ABC的内切圆为球的大圆,
∴r=$\frac{5+12-13}{2}$=2.
∴棱柱的高为2r=4.
∴棱柱的表面积S=2×$\frac{1}{2}×5×12$+(5+12+13)×4=180.
故选:B.
点评 本题考查了棱柱的结构特征,棱柱与内切球的关系,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.一物体在力F(x)=3x2-2x+5(力单位:N,位移单位:m)作用下沿与力F(x)相同的方向由x=5m直线运动到x=10m所做的功是( )
| A. | 925J | B. | 850J | C. | 825J | D. | 800J |
2.若直线l1:(2m+1)x-4y+3m=0与直线l2:x+(m+5)y-3m=0平行,则m的值为( )
| A. | $-\frac{9}{2}或-1$ | B. | $-\frac{9}{2}$ | C. | $-\frac{19}{2}$ | D. | -1 |
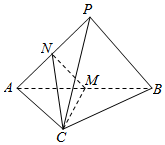 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.