题目内容
17.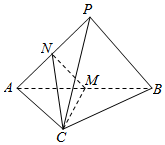 如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.
如图,在三棱锥P-ABC中,平面PAB⊥平面ABC,PA⊥PB,M,N分别为AB,PA的中点.(1)求证:PB∥平面MNC;
(2)若AC=BC,求证:PA⊥平面MNC.
分析 (1)根据中位线定理可得MN∥PB,故而PB∥平面MNC.
(2)由三线合一可得CM⊥AB,再有面面垂直得出CM⊥平面PAB,故CM⊥PA,由AP⊥PB,MN∥PB可得PA⊥MN,故而PA⊥平面MNC.
解答 证明:(1)∵M,N分别为AB,PA的中点,
∴MN∥PB,又MN?平面MNC,PB?平面MNC,
∴PB∥平面MNC.
(2)∵AC=BC,M是AB中点,
∴CM⊥AB,
又∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,CM?平面ABC,
∴CM⊥平面PAB,∵AP?平面PAB,
∴AP⊥CM.
∵PA⊥PB,MN∥PB,
∴PA⊥MN,
又MN?平面MNC,CM?平面MNC,MN∩CM=M,
∴PA⊥平面MNC.
点评 本题考查了线面平行的判定,面面垂直的性质和线面垂直的判定,属于中档题.

练习册系列答案
相关题目
5.一物体沿直线以v=3t+2(t单位:s,v单位:m/s)的速度运动,则该物体在3s~6s间的运动路程为( )
| A. | 46m | B. | 46.5m | C. | 87m | D. | 47m |
12.在直三棱柱ABC-A1B1C1中,BC⊥AC,AC=12,BC=5,若一个球和它的各个面都相切,则该三棱柱的表面积为( )
| A. | 60 | B. | 180 | C. | 240 | D. | 360 |
4.已知直线a,b都与平面α相交,则a,b的位置关系是( )
| A. | 平行 | B. | 相交 | C. | 异面 | D. | 以上都有可能 |
5.已知函数$y={log_a}({x^2}-ax+\frac{1}{2})$,对任意的x1,x2∈[1,+∞),且x1≠x2时,满足$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>0$,则实数a的取值范围是( )
| A. | $(1,\frac{3}{2})$ | B. | $({\frac{3}{2},+∞}]$ | C. | (1,2] | D. | [2,+∞) |