题目内容
15.已知P是椭圆C:$\frac{x^2}{4}+\frac{y^2}{3}$=1上的任一点,Q是与椭圆C共焦点且实轴长为1的双曲线上的任一点,从焦点F1引∠F1QF2的角平分线的垂线,垂足为M,则P,M两点间的最大距离为$\frac{5}{2}$.分析 点F1关于∠F1QF2的角平分线QM的对称点N在直线F2Q上,故|F2N|=|QF2|+|QF1|=1,又OM是△F2F1N的中位线,故|OM|=$\frac{1}{2}$,由此可以判断出点M的轨迹,进而可求P,M两点间的最大距离.
解答 解:如图,由椭圆C:$\frac{x^2}{4}+\frac{y^2}{3}$=1,得F1(-1,0),F2(1,0).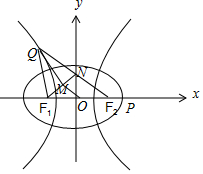
∴双曲线的焦点坐标也为F1(-1,0),F2(1,0).
点F1关于∠F1QF2的角平分线QM的对称点N在直线F2PQ上,
故|F2N|=|QF2|+|QF1|=1,
又OM是△F2F1N的中位线,故|OM|=$\frac{1}{2}$,
∴点M的轨迹是以原点为圆心,$\frac{1}{2}$为半径的圆,
∴P是椭圆长轴的一个端点时,P,M两点间的距离最大,最大值为$\frac{1}{2}$+2=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题给出椭圆上动点P,求点M的轨迹方程,着重考查了椭圆、双曲线的定义和简单几何性质,以及等腰三角形“三线合一”等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若$\frac{1+2i}{a+bi}=1+i$,其中a、b为实数,则a+b的值等于( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
3.执行图中程序框图,如果输入x1=2,x2=3,x3=7,则输出的T值为( )


| A. | 0 | B. | 4 | C. | 2 | D. | 3 |
10.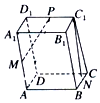 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
 如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )
如图所示,在平行六面体ABCD-A1B1C1D1中,设$\overrightarrow{A{A_1}}=\overrightarrow a$,$\overrightarrow{AB}=\overrightarrow b$,$\overrightarrow{AD}=\overrightarrow c$,M,N,P分别是AA1,BC,C1D1的中点,则$\overrightarrow{MP}+\overrightarrow{N{C_1}}$=( )| A. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{3}{2}\overrightarrow c$ | B. | $\overrightarrow a+\frac{1}{2}\overrightarrow c$ | C. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ | D. | $\frac{3}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\frac{1}{2}\overrightarrow c$ |
20.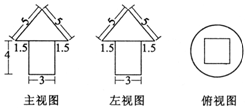 如图是一个几何体的三视图,尺寸如图所示,(单位:cm),则这个几何体的体积是( )
如图是一个几何体的三视图,尺寸如图所示,(单位:cm),则这个几何体的体积是( )
 如图是一个几何体的三视图,尺寸如图所示,(单位:cm),则这个几何体的体积是( )
如图是一个几何体的三视图,尺寸如图所示,(单位:cm),则这个几何体的体积是( )| A. | (10π+36)cm3 | B. | (11π+35)cm3 | C. | (12π+36)cm3 | D. | (13π+34)cm3 |
7.已知函数f(x)=-3lnx+ax2+bx(a>0,b∈R),若对任意x>0都有f(x)≥f(3)成立,则( )
| A. | lna>-b-1 | B. | lna≥-b-1 | C. | lna≤-b-1 | D. | lna<-b-1 |
4.若函数f( x)=ax3-bx+c为奇函数,则c=( )
| A. | 0 | B. | 1 | C. | -1 | D. | -2 |
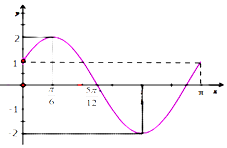 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,$|ϕ|<\frac{π}{2}$)的部分图象如图所示.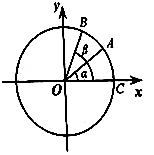 如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).
如图,在平面直角坐标系中,以原点为圆心,单位长度为半径的圆上有两点A($\frac{4}{5}$,$\frac{3}{5}$),B($\frac{5}{13}$,$\frac{12}{13}$).