题目内容
已知tanα≠0,用tanα表示sinα为 .
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:先利用同角三角函数间的基本关系表示出cos2α,即可表示出sinα.
解答:
解:∵sin2α+cos2α=1,
∴sin2α=1-cos2α,
又tanα=
,
∴tan2α=
=
=
-1,
∵
=1+tan2α,
∴cos2α=
,
∵tanα≠0,∴角α的终边不在坐标轴上,
∴cosα=
,
则sinα=cosαtanα=
.
故答案为:sinα=
∴sin2α=1-cos2α,
又tanα=
| sinα |
| cosα |
∴tan2α=
| sin2α |
| cos2α |
| 1-cos2α |
| cos2α |
| 1 |
| cos2α |
∵
| 1 |
| cos2α |
∴cos2α=
| 1 |
| 1+tan2α |
∵tanα≠0,∴角α的终边不在坐标轴上,
∴cosα=
|
则sinα=cosαtanα=
|
故答案为:sinα=
|
点评:此题考查了同角三角函数间基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
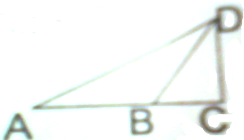 如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100
如图,某人在电视塔CD的一侧A处测得塔顶的仰角为30°,向前走了100
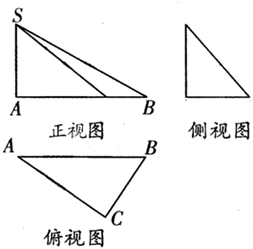 已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )
已知三棱锥S-ABC的三视图如图所示,其中俯视图中AC⊥BC,在原三棱锥中给出下列命题:①BC⊥平面SAC;②平面SBC⊥平面SAB;③SB⊥AC.其中所有正确命题是( )