题目内容
如图甲，矩形ABCD，（AB＞AD）的周长是24，把△ABC沿AC向△ADC折叠，AB折过去后交DC于点P，得到图乙，设AB=x，
（1）设PC=a，试用x表示出a；
（2）把△ADP的面积S表示成x的函数，并求出该函数的最大值及相应的x值．
（1）设PC=a，试用x表示出a；
（2）把△ADP的面积S表示成x的函数，并求出该函数的最大值及相应的x值．
考点：函数最值的应用,函数解析式的求解及常用方法,基本不等式
专题：不等式的解法及应用
分析：（1）本题充分利用勾股定理，找出a与x的数量关系；（2）用三角形面积公式，表示出面积的函数，再利用基本不等式求出面积的最大值．
解答：
（1）∵AB=x，矩形周长为24，
∴AD=12-x，AB折过去后，PC=a，
则PA=a，DP=x-a，在Rt△ADP中，（12-x）2+（x-a）2=a2
解得：a=
．
（2）DP=x-a=
．
所以Rt△ADP的面积S=
(12-x)•
=6×
=6[-(x+
)+18]．
由
，得：6＜x＜12．
由基本不等式，得：x+
≥2
，当且仅当x=6
取等号．
由不等式的性质，得：S≤6[-2
+18]=108-72
综上，当x=6
时△ADP的最大面积是108-72
．
故本题答案为：（1）得：a=
；（2）当x=6
时，△ADP的最大面积是108-72
．
∴AD=12-x，AB折过去后，PC=a，
则PA=a，DP=x-a，在Rt△ADP中，（12-x）2+（x-a）2=a2
解得：a=
| x2-12x+72 |
| x |
（2）DP=x-a=
| 12x-72 |
| x |
所以Rt△ADP的面积S=
| 1 |
| 2 |
| 12x-72 |
| x |
| -x2+18x-72 |
| x |
| 72 |
| x |
由
|
由基本不等式，得：x+
| 72 |
| x |
| 72 |
| 2 |
由不等式的性质，得：S≤6[-2
| 72 |
| 2 |
综上，当x=6
| 2 |
| 2 |
故本题答案为：（1）得：a=
| x2-12x+72 |
| x |
| 2 |
| 2 |
点评：本题属于应用题，考查了基本不等式的知识和数学建模的能力，解题时要注意不等式取等号的条件．对学生的能力要求较高，属于中档题．
练习册系列答案
愉快的寒假南京出版社系列答案
相关题目
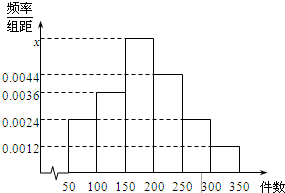从某工厂抽取50名工人进行调查，发现他们一天加工零件的个数在50至350个之间，现按生产的零件个数将他们分成六组，第一组[50，100），第二组[100，150），第三组[150，200），第四组[200，250），第五组[200，250），第六组[300，350），相应的样本频率分布直方图如图所示：