题目内容
10.在△ABC中,A、B、C所对的边分别是a、b、c,且满足下列关系:sin2B≤sin2A+sin2C-sinAsinC.(1)求证:0<B$≤\frac{π}{3}$.
(2)求函数y=$\frac{1+sin2B}{sinB+cosB}$的值域.
分析 (1)由正弦定理和不等式的性质可得cosB≥$\frac{1}{2}$,可得0<B$≤\frac{π}{3}$;
(2)由三角函数公式化简可得y=$\sqrt{2}$sin(B+$\frac{π}{4}$),由B的范围易得函数的值域.
解答 解:(1)∵△ABC中sin2B≤sin2A+sin2C-sinAsinC,
∴由正弦定理可得b2≤a2+c2-ac,即a2+c2-b2≥ac,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$≥$\frac{1}{2}$,∴0<B$≤\frac{π}{3}$;
(2)y=$\frac{1+sin2B}{sinB+cosB}$=$\frac{si{n}^{2}B+co{s}^{2}B+2sinBcosB}{sinB+cosB}$
=$\frac{(sinB+cosB)^{2}}{sinB+cosB}$=sinB+cosB=$\sqrt{2}$sin(B+$\frac{π}{4}$),
∵0<B$≤\frac{π}{3}$,∴$\frac{π}{4}$<B+$\frac{π}{4}$≤$\frac{7π}{12}$,
∴$\frac{\sqrt{2}}{2}$<sin(B+$\frac{π}{4}$)≤1,
∴1<$\sqrt{2}$sin(B+$\frac{π}{4}$)≤$\sqrt{2}$,
∴函数的值域为(1,$\sqrt{2}$]
点评 本题考查正余弦定理解三角形,涉及三角函数的值域,属中档题.

练习册系列答案
相关题目
20.执行如图所示的程序框图,输出的结果是( )
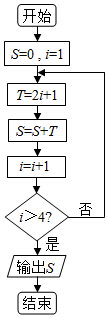

| A. | 15 | B. | 21 | C. | 24 | D. | 35 |
19.下列函数在区间(0,+∞)上为增函数的是( )
| A. | y=cosx | B. | y=2x | C. | y=2-x2 | D. | y=${log}_{\frac{1}{3}}$x |