题目内容

15．已知f（x）=$\left\{\begin{array}{l}{lo{g}_{0.5}x，x＞0}\\{-{x}^{2}-4x，x＜0}\end{array}\right.$，则f（f（-2））=-2．

分析 根据已知中f（x）=$\left\{\begin{array}{l}{lo{g}_{0.5}x，x＞0}\\{-{x}^{2}-4x，x＜0}\end{array}\right.$，将x=-2代入可得答案．

解答 解：∵f（x）=$\left\{\begin{array}{l}{lo{g}_{0.5}x，x＞0}\\{-{x}^{2}-4x，x＜0}\end{array}\right.$，
∴f（-2）=4，
f（f（-2））=f（4）=-2，
故答案为：-2

点评 本题考查的知识点是分段函数的应用，函数求值，难度中档．

练习册系列答案
相关题目
10．在△ABC中，A、B、C所对的边分别是a、b、c，且满足下列关系：sin2B≤sin2A+sin2C-sinAsinC．
（1）求证：0＜B$≤\frac{π}{3}$．
（2）求函数y=$\frac{1+sin2B}{sinB+cosB}$的值域．
11．将函数f（x）=sin（2x+$\frac{π}{6}$）的图象向左平移φ（0＜φ＜$\frac{π}{2}$）个单位得到y=g（x）的图象，|f（x1）-g（x2）|=2的x1，x2，|x1-x2|min=$\frac{π}{4}$，则φ的值是$\frac{π}{4}$．
3．（题类A）双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0），过焦点F1的弦AB长为m（A，B在同一支上），另一个焦点为F2，则△ABF2的周长为（　　）
A．4a-2mB．4aC．4a+mD．4a+2m
10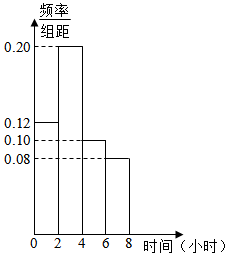．研究人员随机调查统计了某地1000名“上班族”每天在工作之余使用手机上网的时间，并将其绘制为如图所示的频率分布直方图．若同一组数据用该区间的中点值作代表，则可估计该地“上班族”每天在工作之余使用手机上网的平均时间是（　　）
A．1.78小时B．2.24小时C．3.56小时D．4.32小时
20．执行如图所示的程序框图，则输出的i值为（　　）
A．3B．4C．5D．6
7．已知函数f（x）=Asin（2x+φ）（A＞0），其中角φ的终边经过点P（-l，1），且0＜φ＜π．则φ=$\frac{3π}{4}$，f（x）的单调减区间为[-$\frac{π}{8}$+kπ，$\frac{3π}{8}$+kπ]（k∈Z）．
4．已知函数$f（x）=\frac{|x+a|}{{{x^2}+1}}$（a∈R）．
（Ⅰ）当a=1时，解不等式f（x）＞1；
（Ⅱ）对任意的b∈（0，1），当x∈（1，2）时，$f（x）＞\frac{b}{x}$恒成立，求a的取值范围．
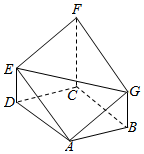5．在如图所示的多面体ABCDEFG中，面ABCD是边长为2的菱形，∠BAD=120°，DE∥CF∥BG，CF⊥面ABCD，AG∥EF，且CF=2 BG=4．
（I）证明：EG∥平面ABCD；
（Ⅱ）求直线CF与平面AEG所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网