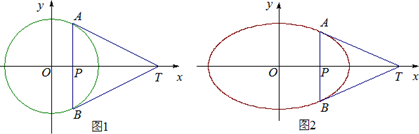
题目内容

设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1、F2离心率e=
3
3
，过点F1且与x轴垂直的直线被椭圆截得的线段长为
4
3
3
．
（1）求椭圆的方程；
（2）过点（0，
2
）且斜率为k的直线l与椭圆相交于A、B两点，且△AF1F2与△BF1F2的面积之和为
3
2
2
，求k的值．
考点：直线与圆锥曲线的综合问题
专题：综合题,圆锥曲线中的最值与范围问题
分析：（1）把x=-c代入椭圆方程可得y=±
b2
a
，由题意得
2b2
a
=
4
3
3
，再由c2=a2-b2，
c
a
=
3
3
联立可求a，b；
（2）设直线AB的方程为：y=kx+
2
，代入
x2
3
+
y2
2
=1，得（2+3k2）x2+6
2
kx=0．易求xB，yB，再由△AF1F2与△BF1F2的面积之和为
3
2
2
，得
1
2
×2×
2
+
1
2
×2×(-yB)=
3
2
2
，从而可得k的方程，解出即可；
解答： 解：（1）将x=-c代入椭圆方程
x2
a2
+
y2
b2
=1，得y=±
b2
a
．
∵过F1且垂直于x轴的直线被椭圆C截得的线段长为
4
3
3
，
∴
2b2
a
=
4
3
3
，即2a=
3
b2．
又∵离心率e=
c
a
=
3
3
，a2=b2+c2，
联立解得∴a2=3，b2=2．
∴椭圆C的方程为
x2
3
+
y2
2
=1．
（2）设直线AB的方程为：y=kx+
2
，代入
x2
3
+
y2
2
=1，得（2+3k2）x2+6
2
kx=0．
设A（0，
2
），B（xB，yB），则xB=
-6
2
k
2+3k2
，yB=kxB+
2
=
2
2
-3
2
k2
2+3k2
，
∵△AF1F2与△BF1F2的面积之和为
3
2
2
，
∴
1
2
×2×
2
+
1
2
×2×(-yB)=
3
2
2
，∴yB=-
2
2
，
∴
2
2
-3
2
k2
2+3k2
=-
2
2
，解得k=±
2
．
点评：该题考查椭圆方程、性质，考查直线与椭圆的位置关系，考查学生分析解决问题的能力．
练习册系列答案
相关题目
圆与椭圆有很多类似的性质，如圆的面积为πr2（r为圆的半径），椭圆的面积为πab（a，b分别为椭圆的长、短半轴的长）．某同学研究了下面几个问题：
（1）圆x2+y2=r2上一点（x0，y0）处的切线方程为x0x+y0y=r2，类似地，请给出椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上一点（x0，y0）处的切线方程（不必证明）；
（2）如图1，TA，TB为圆x2+y2=r2的切线，A，B为切点，OT与AB交于点P，则OP•OT=r2．如图2，TA，TB为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上的切线，A，B为切点，OT与AB交于点P，请给出椭圆中的类似结论并证明．

（3）若过椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上外一点M（s，t）作两条直线与椭圆切于A，B两点，且AB恰好过椭圆的左焦点，求证：点M在一条定直线上．
已知f（x）=（1-tanx）（1+sin2x+cos2x）-3
（Ⅰ）求f（x）的定义域、值域和最小正周期；
（Ⅱ）若f（
α
2
）-f（
α
2
+
π
4
）=
6
，其中α∈（0，
π
2
），求α．
若函数f（x）=
a2-1
x2+（a-1）x+
2
a+1
的定义域为R，求a的取值范围．
已知椭圆C的中心在坐标原点，对称轴为坐标轴，焦点在x轴上，有一个顶点为A（-4，0），
2a2
c
=16．
（1）求椭圆C的方程：
（2）过点B（-1，0）作直线l与椭圆C交于E、F两点，线段EF的中点为M，求直线MA的斜率k的取值范围．
7名男生5名女生中选5人，分别求符合下列的选法总数．（以下问题全部用数字作答）
（1）A，B必须当选；
（2）A，B不全当选；
（3）选取3名男生和2名女生分别担任班长，体育委员等5种不同的工作，但体育必须有男生来担任，班长必须有女生来担任．
已知抛物线D的顶点是椭圆
x2
4
+
y2
3
=1的中心，焦点与该椭圆的右焦点重合
（1）求抛物线D的方程；
（2）已知动直线l过点P（4，0），交抛物D于A，B两点，坐标原点O为PQPQ中点，求证∠AQP=∠BQP．
正方体ABCD-A1B1C1D1中，二面角A-CD-A1的大小为
 
．
复数2-3i（i是虚数单位）的实部、虚部分别是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网