题目内容
 如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°.已知PB=PD=2,PA=
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°.已知PB=PD=2,PA=| 6 |
(Ⅰ)证明:BD⊥面PAC
(Ⅱ)若E为PA的中点,求三菱锥P-BCE的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(Ⅰ)连接BD,AC交于O点,分别证明出PO⊥BD,BD⊥AC,根据线面垂直的判定定理证明出BD⊥平面PAC.
(Ⅱ)先证明出△ABD≌△PBD,求得PO,根据勾股定理证明出AC⊥PO,求得△PAC的面积,最后根据VP-BCE=VB-PEC=
VB-PAC求得答案.
(Ⅱ)先证明出△ABD≌△PBD,求得PO,根据勾股定理证明出AC⊥PO,求得△PAC的面积,最后根据VP-BCE=VB-PEC=
| 1 |
| 2 |
解答:
(Ⅰ)证明:连接BD,AC交于O点,
∵PB=PD,
∴PO⊥BD,
又ABCD是菱形,
∴BD⊥AC,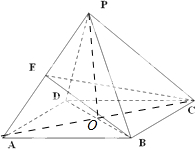
∵PO?平面PAC,AC?平面PAC,AC∩PO=O,
∴BD⊥平面PAC.
(Ⅱ)则AC=2
,
∵△ABD和△PBD的三边长均为2,
∴△ABD≌△PBD,
∴AO=PO=
,
∴AO2+PO2=PA2,
∴AC⊥PO,
S△PAC=
•AC•PO=3,
VP-BCE=VB-PEC=
VB-PAC=
•
•S△PAC•BO=
×
×3×1=
.
∵PB=PD,
∴PO⊥BD,
又ABCD是菱形,
∴BD⊥AC,

∵PO?平面PAC,AC?平面PAC,AC∩PO=O,
∴BD⊥平面PAC.
(Ⅱ)则AC=2
| 3 |
∵△ABD和△PBD的三边长均为2,
∴△ABD≌△PBD,
∴AO=PO=
| 3 |
∴AO2+PO2=PA2,
∴AC⊥PO,
S△PAC=
| 1 |
| 2 |
VP-BCE=VB-PEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
点评:本题主要考查了线面垂直的判定问题,三棱锥的体积计算.解题过程中注重了对学生基础定理的考查.

练习册系列答案
相关题目
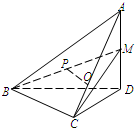 如图在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2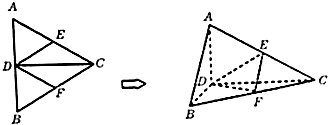
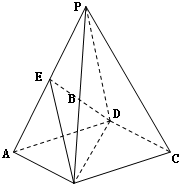 如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证:
如图,在四棱柱P-ABCD中,底面ABCD是矩形,E是棱PA的中点,PD⊥BC.求证:
 如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使
如图,在⊙O的直径AB的延长线上任取一点C,过点C引直线与⊙O交于点D、E,在⊙O上再取一点F,使