题目内容
 如图为函数f(x)=Asin(ωx+φ)(其中ω>0,0≤φ≤
如图为函数f(x)=Asin(ωx+φ)(其中ω>0,0≤φ≤| π |
| 2 |
A、-
| ||||
B、-
| ||||
| C、-1 | ||||
| D、1 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由函数的最值求出A,点A与点B两点之间的距离为5,求得ω,由特殊点的坐标求φ,从而求得函数的解析式.
解答:
解:由题意可得,振幅A=2,根据点A与点B两点之间的距离为5,
可得
=5,求得ω=
.
再把点(0,1)代入函数的解析式可得 2sinφ=1,sinφ=
.
再由0≤φ≤
,可得φ=
,
∴f(x)=2sin(
x+
),
∴f(-1)=2sin(-
)=-1,
故选:C.
可得
42+(
|
| π |
| 3 |
再把点(0,1)代入函数的解析式可得 2sinφ=1,sinφ=
| 1 |
| 2 |
再由0≤φ≤
| π |
| 2 |
| π |
| 6 |
∴f(x)=2sin(
| π |
| 3 |
| π |
| 6 |
∴f(-1)=2sin(-
| π |
| 6 |
故选:C.
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由点A与点B两点之间的距离为5求出ω,由特殊点的坐标求φ,属于中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
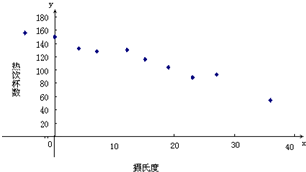 有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程
有一个食品商店为了调查气温对热饮销售的影响,经过调查得到关于卖出的热饮杯数与当天气温的数据如下表,绘出散点图如图.通过计算,可以得到对应的回归方程 |
| y |
| A、气温与热饮的销售杯数之间成正相关 | ||
| B、当天气温为2°C时,这天大约可以卖出143杯热饮 | ||
| C、当天气温为10°C时,这天恰卖出124杯热饮 | ||
D、由于x=0时,
|
 一几何体的三视图如图所示,则该几何体的体积为( )
一几何体的三视图如图所示,则该几何体的体积为( )A、
| ||
B、
| ||
C、(16+4
| ||
D、
|
若变量x,y满足约束条件
,则目标函数z=3x-y的最小值为( )
|
| A、-4 | ||
| B、0 | ||
C、
| ||
| D、4 |