题目内容
若直线y=kx-1与椭圆
+
=1相切,则a的取值范围 ,k的取值范围 .
| x2 |
| 4 |
| y2 |
| a |
考点:直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:直线y=kx-1,恒过点(0,-1),直线y=kx-1与椭圆
+
=1相切,可判断点(0,-1)在椭圆外,可求得a的范围.
根据方程组的解判断k的范围.
| x2 |
| 4 |
| y2 |
| a |
根据方程组的解判断k的范围.
解答:
解:(1)∵直线y=kx-1,恒过点(0,-1),直线y=kx-1与椭圆
+
=1相切,
∴点(0,-1)在椭圆外,即
>1,a∈(0,1]
(2)联立方程组得:(a+4k2)x2-8kx4-4a=0,
△=64k2a+16a2-16a=0,
a=1-4k2,即0<1-4k2<1,
解得:-
<k<
,
所以实数a的取值范围 (0,1],k的取值范围(-
,
),
故答案为:(0,1],(-
,
),
| x2 |
| 4 |
| y2 |
| a |
∴点(0,-1)在椭圆外,即
| 1 |
| a |
(2)联立方程组得:(a+4k2)x2-8kx4-4a=0,
△=64k2a+16a2-16a=0,
a=1-4k2,即0<1-4k2<1,
解得:-
| 1 |
| 2 |
| 1 |
| 2 |
所以实数a的取值范围 (0,1],k的取值范围(-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(0,1],(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题综合考查了,点,直线与椭圆的位置关系,结合方程,不等式,求解.

练习册系列答案
相关题目
函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x.若在区间[-2,2]上方程ax+a-f(x)=0恰有三个不相等的实数根,则实数a的取值范围是( )
| A、[0,1) |
| B、[0,2] |
| C、[1,+∞) |
| D、[2,+∞) |
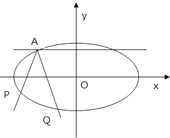 如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).
如图,焦点在x轴的椭圆,离心率A,且过点A(-2,1),由椭圆上异于点A的P点发出的光线射到A点处被直线Q反射后交椭圆于Q点(Q点与P点不重合).