题目内容
13．如果P：关于x的不等式x2+2ax+4＞0对一切 x∈R都成立，q：关于 x 的方程 4x2+4（a-2）x+1=0无实数根，且P与q中有且只有一个是真命题，求实数a的取值范围．分析 当命题p，q是真命题时，分别求得a的范围，可得这2个命题中只有一个是真命题时，实数a的取值范围
解答 解：若命题p为真，则△=（2a）2-16＜0⇒-2＜a＜2．
若命题q为真，△=[4（a-2）]2-16＜0，⇒1＜a＜3．
当p为真q为假时：⇒-2＜a＜2且a≤1或a≥3⇒-2＜a≤1
当p为假q为真时：⇒-a≤-2或a≥2且1＜a＜3⇒2≤a＜3
综上：实数a的取值范围为：⇒-2＜a≤1或2≤a＜3
点评 本题主要考查了命题的真假的判断和应用，二次函数的性质，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
1．
如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A′∉平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列说法，不正确的是（ ）
如图，边长为a的等边三角形ABC的中线AF与中位线DE交于点G，已知△A′DE（A′∉平面ABC）是△ADE绕DE旋转过程中的一个图形，有下列说法，不正确的是（ ）| A． | 平面A′FG⊥平面ABC | |
| B． | BC∥平面A′DE | |
| C． | 三棱锥A′-DEF的体积最大值为$\frac{1}{64}{a^3}$ | |
| D． | 直线DF与直线A′E有可能异面 |
18．长方形ABCD中，AB=2，BC=1，F是线段DC上一动点，且0＜FC＜1．将△AFD沿AF折起，使平面AFD⊥平面ABC，在平面ABD内作DK⊥AB于K，设AK=t，则t的值可能为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
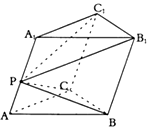如图，P为三棱柱ABC-A1B1C1的侧棱AA1上的一个动点，若四棱锥P-BCC1B1的体积为V，则三棱柱ABC-A1B1C1的体积为$\frac{3}{2}V$（用V表示）
2．命题p：?x0∈R，x0≤2的否定是（ ）
| A． | ￢p：?x∈R，x≤2 | B． | ￢p：?x∈R，x＞2 | C． | ￢p：?x∈R，x＞2 | D． | ￢p：?x∈R，x≤2 |