题目内容
18.长方形ABCD中,AB=2,BC=1,F是线段DC上一动点,且0<FC<1.将△AFD沿AF折起,使平面AFD⊥平面ABC,在平面ABD内作DK⊥AB于K,设AK=t,则t的值可能为( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 此题的破解可采用二个极端位置法,即对于F位于DC的中点时与随着F点到C点时,分别求出此两个位置的t值即可得到所求的答案.
解答 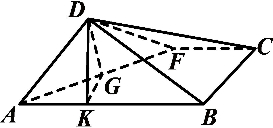 解:如图,过D作DG⊥AF,垂足为G,连接GK,
解:如图,过D作DG⊥AF,垂足为G,连接GK,
∵平面AFD⊥平面ABC,又DK⊥AB,
∴AB⊥平面DKG,
∴AB⊥GK.
容易得到,当F接近E点时,K接近AB的中点,
∵长方形ABCD中,AB=2,BC=1,E为CD的中点,
∴计算可得:AG=$\frac{\sqrt{2}}{2}$,DG=$\frac{\sqrt{2}}{2}$,DK=$\frac{\sqrt{3}}{2}$,KG=$\frac{1}{2}$,
∴t=AK=$\frac{1}{2}$,
当F接近C点时,可得三角形ADG和三角形ADC相似.
∴$\frac{AG}{1}=\frac{1}{\sqrt{5}}$,可解得AG=$\frac{\sqrt{5}}{5}$,
可得三角形AKG和三角形ABC相似.
∴$\frac{\frac{\sqrt{5}}{5}}{\sqrt{5}}=\frac{t}{2}$,解得t=$\frac{2}{5}$,
∴t的取值范围是($\frac{2}{5}$,$\frac{1}{2}$).
故选:B.
点评 考查空间图形的想象能力,及根据相关的定理对图形中的位置关系进行精准判断的能力.

练习册系列答案
相关题目
8.不等式组$\left\{\begin{array}{l}{x≥0}\\{x+3y≥4}\\{2x+y≤3}\end{array}\right.$所表示的平面区域的面积为$\frac{5}{6}$.
3.已知α,β是相异两平面,m,n是相异两直线,则下列命题中不正确的是 ( )
| A. | 若m∥n,m⊥α,则n⊥α | B. | 若m⊥α,m⊥β,则α∥β | ||
| C. | 若m∥α,α∩β=n,则m∥n | D. | 若m⊥α,m?β,则α⊥β |
7. 如图某空间几何体的正视图和俯视图分别为边长为2的正方形和正三角形,则该空间几何体的外接球的表面积为( )
如图某空间几何体的正视图和俯视图分别为边长为2的正方形和正三角形,则该空间几何体的外接球的表面积为( )
 如图某空间几何体的正视图和俯视图分别为边长为2的正方形和正三角形,则该空间几何体的外接球的表面积为( )
如图某空间几何体的正视图和俯视图分别为边长为2的正方形和正三角形,则该空间几何体的外接球的表面积为( )| A. | $\frac{16π}{3}$ | B. | $\frac{28π}{3}$ | C. | 16π | D. | 21π |
1.焦点在x轴上的椭圆${x^2}-\frac{y^2}{k}=1$的离心率为$\frac{1}{2}$,则焦距为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 1 |