题目内容
10.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,(x<1)}\\{{e}^{x},(x≥1)}\end{array}\right.$,若函数g(x)=f(x)-kx恰有一个零点,则k的取值范围是( )| A. | (e,+∞) | B. | (-∞,e) | C. | (-∞,$\frac{1}{e}$) | D. | [0,e) |
分析 利用函数的零点,转化为方程根,转化为两个函数的图象的交点,求出一个零点,然后求解k的范围即可.
解答  解:∵函数函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,(x<1)}\\{{e}^{x},(x≥1)}\end{array}\right.$,
解:∵函数函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,(x<1)}\\{{e}^{x},(x≥1)}\end{array}\right.$,
∴f(0)=0,
∴x=0是函数y=f(x)-kx的一个零点,
函数g(x)=f(x)-kx恰有一个零点,可得:y=f(x)与y=kx的图象如图:
当x<1时,由f(x)=kx,两个函数只有一个交点,则k≤1;
当x≥1时,y=ex,是增函数,x=1时,函数的最小值为:e,
可知k<e.
f'(x)=ex∈(1,+∞),
∴要使函数y=f(x)-kx在x>0时有一个零点,
则k>1,
∴k>1,
即实数k的取值范围是(-∞,e),
故选:B.
点评 本题考查的知识点是函数零点及零点的个数,二次函数的图象和性质,指数型函数的图象和性质,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.三棱柱ABC-A1B1C1的底面是直角三角形,侧棱垂直于底面,面积最大的侧面是正方形,且正方形的中心是该三棱柱的外接球的球心,若外接球的表面积为8π,则三棱柱ABC-A1B1C1的体积的最大值为( )
| A. | 2 | B. | 3 | C. | $2\sqrt{2}$ | D. | 4 |
18.某几何体的三视图如图所示,其中俯视图中半圆半径为$\sqrt{2}$,则该几何体的体积是( )
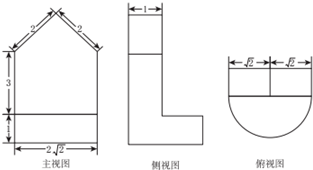

| A. | $2π+8\sqrt{2}+2$ | B. | $2π+8\sqrt{2}+1$ | C. | $π+8\sqrt{2}+1$ | D. | $π+8\sqrt{2}+2$ |
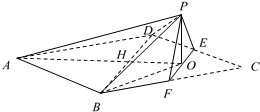 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.