题目内容
3.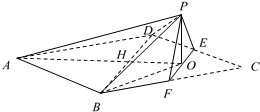 边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.
边长为4的菱形ABCD中,满足∠DCB=60°,点E,F分别是边CD和CB的中点,AC交BD于点H,AC交EF于点O,沿EF将△CEF翻折到△PEF的位置,使平面PEF⊥平面ABD,连接PA,PB,PD,得到如图所示的五棱锥P-ABFED.(Ⅰ)求证:BD⊥PA;
(Ⅱ)求点D到平面PBF的距离.
分析 (Ⅰ)根据面面垂直的性质定理即可证明BD⊥PA;
(Ⅱ)设点D到平面PBF的距离为h,由等体积可得点D到平面PBF的距离.
解答 (Ⅰ)证明:∵平面PEF⊥平面ABD,平面PEF∩平面ABD=EF,PO?PEF,
∴PO⊥平面ABD
则PO⊥BD,
又AO⊥BD,AO∩PO=O,AO?APO,PO?APO,
∴BD⊥平面APO,
∵AP?平面APO,∴BD⊥PA….(6分)
(Ⅱ)解:由题意,O到BC的距离为$\frac{\sqrt{3}}{2}$,PO=$\sqrt{3}$,
∴P到BC的距离为$\sqrt{\frac{3}{4}+3}$=$\frac{\sqrt{15}}{2}$,
设点D到平面PBF的距离为h,则由等体积可得$\frac{1}{3}×\frac{1}{2}×2×\frac{\sqrt{15}}{2}h=\frac{1}{3}×\frac{1}{2}×4×\sqrt{3}×\sqrt{3}$,
∴h=$\frac{{4\sqrt{15}}}{5}$…(12分)
点评 本题主要考查线线垂直的判定以及点D到平面PBF的距离,考查等体积方法的运用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.若$\overrightarrow{e_1}$,$\overrightarrow{e_2}$是平面内的一组基底,则以下的四组向量中不能作为一组基底的是( )
| A. | $\overrightarrow{e_1}$,2$\overrightarrow{e_2}$ | B. | $\overrightarrow{e_1}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ | ||
| C. | -$\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ | D. | $\overrightarrow{e_1}+\overrightarrow{e_2}$,$\overrightarrow{e_1}-\overrightarrow{e_2}$ |
10.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,(x<1)}\\{{e}^{x},(x≥1)}\end{array}\right.$,若函数g(x)=f(x)-kx恰有一个零点,则k的取值范围是( )
| A. | (e,+∞) | B. | (-∞,e) | C. | (-∞,$\frac{1}{e}$) | D. | [0,e) |
 如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为1的正方形,侧棱AA1=2,E是侧棱BB1的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面是边长为1的正方形,侧棱AA1=2,E是侧棱BB1的中点. S(1,1)是抛物线L:y2=2px(p>0)上一点,以S为圆心,r为半径的圆,与x轴正半轴相交于A,B两点,连结并延长SA,SB,分别交椭圆L于C,D两点(如图所示).
S(1,1)是抛物线L:y2=2px(p>0)上一点,以S为圆心,r为半径的圆,与x轴正半轴相交于A,B两点,连结并延长SA,SB,分别交椭圆L于C,D两点(如图所示).