题目内容
19.已知f(x)=$\frac{a}{x}$+lnx(a∈R).(1)当a=3时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)研究y=f(x)在定义域内的单调性;
(3)如果f(x)≥0在定义域内恒成立,求a的取值范围.
分析 (1)根据导数的几何意义即可求出曲线y=f(x)在点(1,f(1))处的切线方程,
(2)先求出函数的导函数,再分类讨论,即可判断函数的单调性,
(3)分离参数,构造函数g(x)=-xlnx,根据导数求出函数的最大值,问题得以解决.
解答 解:(1)a=3时,f(x)=$\frac{3}{x}$+lnx,
∴f′(x)=-$\frac{3}{{x}^{2}}$+$\frac{1}{x}$,
∴f′(1)=-3+1=-2,f(1)=3,
∴曲线y=f(x)在点(1,f(1))处的切线方程为y-3=-2(x-1),即为y=-2x+5;
(2)∵${f^'}(x)=-\frac{a}{x^2}+\frac{1}{x}=\frac{x-a}{x^2}$,
当a≤0时,f(x)在(0,+∞)上递增,
当a>0时,f(x)在(a,+∞)上递增,在(0,a)上递减.
(3)∵f(x)≥0在定义域内恒成立,
∴a≥-xlnx对x∈(0,+∞)恒成立,
设g(x)=-xlnx,
∴g′(x)=-lnx-1,
令g′(x)=0,解得x=$\frac{1}{e}$,
当g′(x)>0时,解得0<x<$\frac{1}{e}$,函数g(x)单调递增,
当g′(x)<0时,解得x>$\frac{1}{e}$,函数g(x)单调递减,
∴g(x)max=g($\frac{1}{e}$)=$\frac{1}{e}$,
∴a≥$\frac{1}{e}$,
故a的取值范围为[$\frac{1}{e}$,+∞).
点评 本题考查了切线方程和函数的单调性以及函数恒成立问题,考查了数学转化思想方法和分类讨论的数学思想方法,属于中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
10.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+4x,(x<1)}\\{{e}^{x},(x≥1)}\end{array}\right.$,若函数g(x)=f(x)-kx恰有一个零点,则k的取值范围是( )
| A. | (e,+∞) | B. | (-∞,e) | C. | (-∞,$\frac{1}{e}$) | D. | [0,e) |
7.抛物线y2=2px的焦点为F,过点F斜率为k的直线交抛物线于A,B两点,以AB为直径的圆与直线k:x=-2相切,则p的值为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 由k的值确定 |
 已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,且二面角D-AE-C的正切值为-2.
已知底面为矩形的四棱锥D-ABCE,AB=1,BC=2,AD=3,DE=$\sqrt{5}$,且二面角D-AE-C的正切值为-2.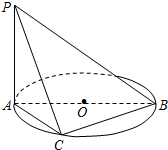 已知PA垂直于以AB为直径的ΘO所在的平面,C是ΘO上异于A,B的动点,PA=1,AB=2,当三棱锥P-ABC取得最大体积时,求:
已知PA垂直于以AB为直径的ΘO所在的平面,C是ΘO上异于A,B的动点,PA=1,AB=2,当三棱锥P-ABC取得最大体积时,求: