题目内容
15.在直角坐标系xOy中,曲线C1的参数方程为 $\left\{\begin{array}{l}x=\sqrt{2}+2t\\ y=-\sqrt{2}+t\end{array}$(t为参数),在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的方程为ρ=$\frac{2}{{\sqrt{1+3{{sin}^2}θ}}}$.(Ⅰ)求曲线C1、C2的直角坐标方程;
(Ⅱ)若A、B分别为曲线C1、C2上的任意点,求|AB|的最小值.
分析 (1)在曲线C1的参数方程中,消去参数t,能得到曲线C1的直角坐标方程;在曲线C2的方程ρ=$\frac{2}{{\sqrt{1+3{{sin}^2}θ}}}$中,极坐标与直角坐标的互化公式能求出曲线C1、C2的直角坐标方程.
(2)设B(2cosθ,sinθ),利用点到直线的距离公式能求出|AB|的最小值.
解答 解:(1)∵在直角坐标系xOy中,曲线C1的参数方程为 $\left\{\begin{array}{l}x=\sqrt{2}+2t\\ y=-\sqrt{2}+t\end{array}$(t为参数),
∴消去参数t,得曲线C1的直角坐标方程为:x-2y-3$\sqrt{2}$=0,
∵在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C2的方程为ρ=$\frac{2}{{\sqrt{1+3{{sin}^2}θ}}}$.
∴ρ2+3ρ2sin2x-4=0,
∴C2的直角坐标方程为x2+4y2=4,即$\frac{{x}^{2}}{4}+{y}^{2}$=1,
${C_1}:x-2y-3\sqrt{2}=0,{C_2}:\frac{x^2}{4}+{y^2}=1$.(6分)
(2)∵A、B分别为曲线C1、C2上的任意点,
∴设B(2cosθ,sinθ),
则$|{AB}|=\frac{{|{2cosθ-2sinθ-3\sqrt{2}}|}}{{\sqrt{5}}}=\frac{{|{2\sqrt{2}cos({θ+\frac{π}{4}})--3\sqrt{2}}|}}{{\sqrt{5}}}$,
当且仅当$θ=2kπ-\frac{π}{4}({k∈Z})$时,
${|{AB}|_{min}}=\frac{{\sqrt{2}}}{{\sqrt{5}}}=\frac{{\sqrt{10}}}{5}$.(12分)
点评 本题考查参数方程、极坐标、平面直角坐标方程的互化,考查两点间距离的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案| A. | (e,+∞) | B. | (-∞,e) | C. | (-∞,$\frac{1}{e}$) | D. | [0,e) |
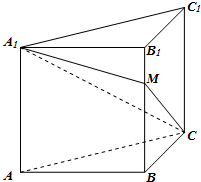 正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M.
正方体ABCD-A1B1C1D1中,沿平面A1ACC1将正方体分成两部分,其中一部分如图所示,过直线A1C的平面A1CM与线段BB1交于点M. 如图:将直角三角形PAO,绕直角边PO旋转构成圆锥,ABCD是⊙O的内接矩形,M为是母线PA的中点,PA=2AO.
如图:将直角三角形PAO,绕直角边PO旋转构成圆锥,ABCD是⊙O的内接矩形,M为是母线PA的中点,PA=2AO.