题目内容

已知矩形ABCD，P为平面ABCD外一点，M、N分别为BC、PD的中点，且满足
MN
=x
AB
+y
AD
+z
AP
，则实数x+y+z的值为
 
．
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：先根据
MN
=
MB
+
BP
+
PN
，再根据M、N分别为BC、PD的中点，以及向量的加减得到
MN
═
1
2
AP
-
AB
，问题得以解决．
解答： 解：∵M、N分别为BC、PD的中点，
∴
PN
=
1
2
PD
，
∵
MN
=
MB
+
BP
+
PN
=-
1
2
BC
+（
AP
-
AB
）+
1
2
PD
，
=-
1
2
AD
+（
AP
-
AB
）+
1
2
（
AD
-
AP
），
=
1
2
AP
-
AB
，
∵
MN
=x
AB
+y
AD
+z
AP
，
∴x=-1，y=0，z=
1
2
，
∴x+y+z=-
1
2
，
故答案为：-
1
2
．
点评：本题主要考查向量的加减的几何意义，正确运算时关键，属于基础题．
练习册系列答案
相关题目
如图所示的多面体中，ABCD是菱形，BDEF是矩形，ED⊥平面ABCD，∠BAD=
π
3
，AD=2．
（Ⅰ）求证：平面FCB∥平面AED；
（Ⅱ）若二面角A-EF-C的大小为
π
3
，求线段ED的长．
△ABC的内角A，B，C对边分别为a，b，c，且满足sinA：sinB：sinC=2：3：4，则
a+b
b+c
=
 
．
已知集合A={（x，y）|y=x2}，B={（x，y）|x-y+2=0}，则A∩B=
 
．
数列
1
2
，-2，
9
2
，-8，
25
2
…的一个通项公式是
 
．
如图，设平面α∩β=EF，AB⊥α，CD⊥α，垂足分别为B，D，若增加一个条件，就能推出BD⊥EF．现有①AC⊥β；②AC∥EF③AC与CD在β内的射影在同一条直线上．那么上述几个条件中能成为增加条件的序号是
 
．
已知函数f（x）=ln（3x）+8x，则
lim
△x→0
f(1-2△x)-f(1)
△x
=
 
．
设函数f（x）是定义在R上的偶函数，且对任意的x∈R恒有f（x+1）=f（x-1），已知当x∈[0，1]时，
f（x）=cos
πx
2
，则以下正确命题的序号是
 

①?x∈R，f（1-x）=f（1+x）；
②函数f（x）在（1，2）上是减函数，在（2，3）上是增函数；
③f（x）的最大值是1，最小值是0；
④f（x）的一个对称中心是（5，0）．
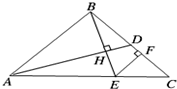等腰直角△ABC中，AD是直角边BC上的中线，BE⊥AD，交AC于E，EF⊥BC，若AB=BC=a，则EF等于（　　）
A、
2
5
a
B、
1
2
a
C、
1
3
a
D、
2
3
a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网