Question

设A、B、C是半径为1的球面上的三点，B、C两点间的球面距离为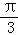，点A与B、C两点间的球面距离均为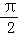，O为球心，

求：（1）∠AOB、∠BOC的大小；

（2）球心O到截面ABC的距离．

Answer 1

（1）∠BOC=，∠AOB=∠AOC=．

（2）

【解析】

试题分析：（1）根据球面距离的定义可得）∠AOB、∠BOC的大小；

（2）欲求球心O到截面ABC的距离，截面圆的圆心为O1，可通过解直角三角形AOO1解决．

【解析】
如图，（1）因为球O的半径为1，B、C两点间的球面距离为，

点A与B、C两点间的球面距离均为，所以∠BOC=，∠AOB=∠AOC=．

（2）因为BC=1，AC=AB=，所以由余弦定理得cos∠BAC=，

sin∠BAC=，设截面圆的圆心为O1，连接AO1，

则截面圆的半径R=AO1，由正弦定理得r==，

所以OO1==．