题目内容
15.某三棱锥的三视图如图所示,该三棱锥的体积是( )
| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | $6+2\sqrt{3}$ |
分析 由三视图可知:该几何体为三棱锥P-ABC,其中PA⊥底面ABC,AB⊥AC,AB=AC=2,PA=2.
解答 解:由三视图可知:该几何体为三棱锥P-ABC,其中PA⊥底面ABC,AB⊥AC,AB=AC=2,PA=2.
∴V=$\frac{1}{3}×2×\frac{1}{2}×{2}^{2}$=$\frac{4}{3}$.
故选:A.
点评 本题考查了三棱锥的三视图、体积的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.双曲线4y2-25x2=100的焦点坐标是( )
| A. | (-5,0),(5,0) | B. | (0,-5),(0,5) | C. | $(-\sqrt{29},0)$,$(\sqrt{29},0)$ | D. | $(0,-\sqrt{29})$,$(0,\sqrt{29})$ |
6.两圆x2+y2+4x-4y=0与x2+y2+2x-12=0的公共弦长等于( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
4.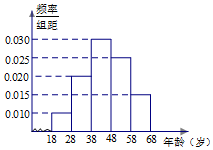 某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68],再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68],再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
(Ⅰ)分别求出a,x的值;
(Ⅱ)第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(III)在( II)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
 某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68],再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为n的样本,并将样本数据分成五组:[18,28),[28,38),[38,48),[48,58),[58,68],再将其按从左到右的顺序分别编号为第1组,第2组,…,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.| 组号 | 分组 | 回答正确的人数 | 回答正确 的人数占本 组的比例 |
| 第1组 | [18,28) | 5 | 0.5 |
| 第2组 | [28,38) | 18 | a |
| 第3组 | [38,48) | 27 | 0.9 |
| 第4组 | [48,58) | x | 0.36 |
| 第5组 | [58,68] | 3 | 0.2 |
(Ⅱ)第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(III)在( II)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
5.已知数列{an}为等差数列,数列{bn}为等比数列,且满足a2016+a2017=π,b20b21=4,则tan$\frac{{a}_{1}+{a}_{4032}}{2+{b}_{19}{b}_{22}}$=( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | 1 | D. | -1 |
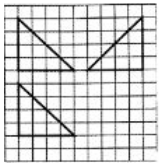 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球面的表面积为48π.
如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的各个顶点在某一个球面上,则该球面的表面积为48π.