题目内容
10.将函数y=sin(x-$\frac{π}{6}$)图象上所有的点( ),可以得到函数y=sin(x+$\frac{π}{6}$)的图象.| A. | 向左平移$\frac{π}{3}$单位 | B. | 向右平移$\frac{π}{3}$单位 | C. | 向左平移$\frac{π}{6}$单位 | D. | 向右平移$\frac{π}{6}$单位 |
分析 直接根据函数y=Asin(ωx+∅)的图象变换规律得出结论.
解答 解:∵y=sin(x+$\frac{π}{6}$)=sin[(x+$\frac{π}{3}$)-$\frac{π}{6}$],
∴将函数y=sin(x-$\frac{π}{6}$)图象上所有的点向左平移$\frac{π}{3}$单位,可以得到函数y=sin(x+$\frac{π}{6}$)的图象.
故选:A.
点评 本题主要考查函数y=Asin(ωx+∅)的图象变换规律,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
20.已知圆C的圆心与点P(-2,1)关于直线y=x+1对称,直线3x+4y-11=0与圆C相交于A,B点,且|AB|=6,则圆C的方程为( )
| A. | x2+(y+1)2=18 | B. | (x+1)2+y2=9 | C. | (x+1)2+y2=18 | D. | x2+(y+1)2=9 |
1.在以“菊韵荆门,荣耀中华”为主题的“中国•荆门菊花展”上,工作人员要将6盆不同品种的菊花排成一排,其中甲,乙在丙同侧的不同排法种数为( )
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
18.设点F1、F2是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点(O为坐标原点),以O为圆心,|F1F2|为直径的圆交双曲线于点M(第一象限).若过点M作x轴的垂线,垂足恰为线段OF2的中点,则双曲线的离心率是( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$ | C. | $\sqrt{3}$+1 | D. | 2 |
19.已知直线的斜率是6,在y轴上的截距是-4,则此直线方程是( )
| A. | 6x-y-4=0 | B. | 6x-y+4=0 | C. | 6x+y+4=0 | D. | 6x+y-4=0 |
14.将一块边长为10的正方形铁片按图1所示的阴影部分裁下,用余下的四个全等的等腰三角形加工成一个底面边长为x的正四棱锥形容器(如图2),则函数f(x)=$\frac{{V}_{E-ABCD}}{x}$的最大值为( )
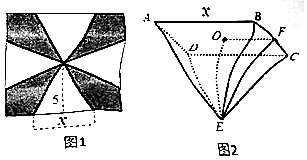

| A. | $\frac{25\sqrt{3}}{6}$ | B. | $\frac{50}{3}$ | C. | $\frac{25}{3}$ | D. | $\frac{125\sqrt{3}}{6}$ |
 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,G分别是PA,PB,BC的中点;
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,G分别是PA,PB,BC的中点;