题目内容
8.已知△ABC的外接圆的半径为$\sqrt{2}$,内角A、B、C的对边分别为a、b、c,向量$\overrightarrow m=(sinA-sinC,b-a)$,$\overrightarrow n=(sinA+sinC,\frac{{\sqrt{2}}}{4}sinB)$,且$\overrightarrow m⊥\overrightarrow n$.(I)求角C;
(II)求△ABC的面积S的最大值,并判断此时△ABC的形状.
分析 (I)根据$\overrightarrow m⊥\overrightarrow n$建立等式关系,利用正余弦定理即可求角C;
(II)根据△ABC的面积S=$\frac{1}{2}$absinC,利用余弦定理和基本不等式求最大,即可判断此时△ABC的形状.
解答 解:向量$\overrightarrow m=(sinA-sinC,b-a)$,$\overrightarrow n=(sinA+sinC,\frac{{\sqrt{2}}}{4}sinB)$,且$\overrightarrow m⊥\overrightarrow n$.
(I)∵$\overrightarrow m⊥\overrightarrow n$,
∴sin2A-sin2C=$\frac{\sqrt{2}}{4}$(a-b)sinB.
由正弦定理可得:sinA=$\frac{a}{2R}$,sinB=$\frac{b}{2R}$,sinC=$\frac{c}{2R}$,
∴a2-c2=(a-b)b.
由余弦定理:cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}=\frac{ab}{2ab}=\frac{1}{2}$.
∵0<C<π,
∴C=$\frac{π}{3}$.
(II)△ABC的面积S=$\frac{1}{2}$absinC,
∵C=$\frac{π}{3}$,R=$\sqrt{2}$,
∴c=2RsinC=$\sqrt{6}$.
由余弦定理:得a2+b2=6+ab.
∵a2+b2≥2ab,(当且仅当a=b是取等)
∴ab≤6.
故得△ABC的面积S=$\frac{1}{2}$absinC$≤\frac{1}{2}×6×\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
∵C=$\frac{π}{3}$,a=b.
此时△ABC为等边三角形.
点评 本题考查了向量垂直的计算和正余弦定理的运用和计算能力.属于基础题.

| A. | 钝角 | B. | 锐角 | ||
| C. | 小于180°的正角 | D. | 第一或第二象限角 |
| A. | 零个 | B. | 一个 | C. | 两个 | D. | 无数个 |

他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )
| A. | 36 | B. | 45 | C. | 99 | D. | 100 |
周率π的近似值为( )
| A. | $\frac{m}{n}$ | B. | $\frac{2m}{n}$ | C. | $\frac{4m}{n}$ | D. | $\frac{6m}{n}$ |
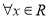 ,
, ;
; ”是假命题,则
”是假命题,则 都是假命题;
都是假命题; ”的否定是“
”的否定是“ ,
, ”
”