题目内容
已知函数f(x)=lnx-mx(m∈R).
(1)若曲线y=f(x)过点P(1,-1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1,x2,求证:x1x2>e2.
(1)若曲线y=f(x)过点P(1,-1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1,x2,求证:x1x2>e2.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)中求出斜率,代入切线方程即可;
(2)中需要讨论m的范围,m的取值范围不一样,求出的最值不同;
(3)中将所证的结论转化为求新函数的单调区间问题得以解决.
(2)中需要讨论m的范围,m的取值范围不一样,求出的最值不同;
(3)中将所证的结论转化为求新函数的单调区间问题得以解决.
解答:
解:(1)因为点P(1,-1)在曲线y=f(x)上,
所以-m=-1,解得m=1.
因为f′(x)=
-1=0,
所以切线的斜率为0,
所以切线方程为y=-1.
(2)因为f′(x)=
-m=
.
①当m≤0时,x∈(1,e),f′(x)>0,
所以函数f (x)在(1,e)上单调递增,
则f (x)max=f (e)=1-me.
②当
≥e,即0<m≤
时,x∈(1,e),f′(x)>0,
所以函数f (x)在(1,e)上单调递增,
则f (x)max=f (e)=1-me.
③当1<
<e,即
<m<1时,
函数f (x)在 (1,
)上单调递增,在(
,e)上单调递减,
则f (x)max=f (
)=-lnm-1.
④当
≤1,即m≥1时,x∈(1,e),f′(x)<0,
函数f (x)在(1,e)上单调递减,
则f (x)max=f (1)=-m.
综上,①当m≤
时,f (x)max=1-me;
②当
<m<1时,f (x)max=-lnm-1;
③当m≥1时,f (x)max=-m.
(3)不妨设x1>x2>0.
因为f (x1)=f (x2)=0,
所以lnx1-mx1=0,lnx2-mx2=0,
可得lnx1+lnx2=m(x1+x2),lnx1-lnx2=m(x1-x2).
要证明x1x2>e2,
即证明lnx1+lnx2>2,也就是m(x1+x2)>2.
因为m=
,
所以即证明
>
,
即ln
>
.
令
=t,则t>1,于是lnt>
.
令ϕ(t)=lnt-
(t>1),
则ϕ′(t)=
-
=
>0.
故函数ϕ(t)在(1,+∞)上是增函数,
所以ϕ(t)>ϕ(1)=0,即lnt>
成立.
所以原不等式成立.
所以-m=-1,解得m=1.
因为f′(x)=
| 1 |
| x |
所以切线的斜率为0,
所以切线方程为y=-1.
(2)因为f′(x)=
| 1 |
| x |
| 1-mx |
| x |
①当m≤0时,x∈(1,e),f′(x)>0,
所以函数f (x)在(1,e)上单调递增,
则f (x)max=f (e)=1-me.
②当
| 1 |
| m |
| 1 |
| e |
所以函数f (x)在(1,e)上单调递增,
则f (x)max=f (e)=1-me.
③当1<
| 1 |
| m |
| 1 |
| e |
函数f (x)在 (1,
| 1 |
| m |
| 1 |
| m |
则f (x)max=f (
| 1 |
| m |
④当
| 1 |
| m |
函数f (x)在(1,e)上单调递减,
则f (x)max=f (1)=-m.
综上,①当m≤
| 1 |
| e |
②当
| 1 |
| e |
③当m≥1时,f (x)max=-m.
(3)不妨设x1>x2>0.
因为f (x1)=f (x2)=0,
所以lnx1-mx1=0,lnx2-mx2=0,
可得lnx1+lnx2=m(x1+x2),lnx1-lnx2=m(x1-x2).
要证明x1x2>e2,
即证明lnx1+lnx2>2,也就是m(x1+x2)>2.
因为m=
| lnx1-lnx2 |
| x1-x2 |
所以即证明
| lnx1-lnx2 |
| x1-x2 |
| 2 |
| x1+x2 |
即ln
| x1 |
| x2 |
| 2(x1-x2) |
| x1+x2 |
令
| x1 |
| x2 |
| 2(t-1) |
| t+1 |
令ϕ(t)=lnt-
| 2(t-1) |
| t+1 |
则ϕ′(t)=
| 1 |
| t |
| 4 |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
故函数ϕ(t)在(1,+∞)上是增函数,
所以ϕ(t)>ϕ(1)=0,即lnt>
| 2(t-1) |
| t+1 |
所以原不等式成立.
点评:本题是关于导数的综合应用,利用导数求斜率,求函数的单调区间以及区间上的最值是最主要的题型之一.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在复平面内,复数
对应的点位于( )
| -3+i |
| 2+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
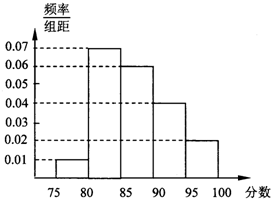 某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查:
某市教育局为了了解高三学生体育达标情况,在某学校的高三学生体育达标成绩中随机抽取100个进行调研,按成绩分组:第l组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示:若要在成绩较高的第3,4,5组中用分层抽样抽取6名学生进行复查: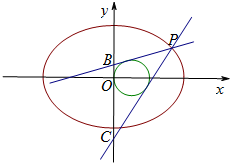 设椭圆E:
设椭圆E: