Question

已知直线kx+y+2=0和以M（-2，1），N（3，2）为端点的线段相交，则实数k的取值范围为

 

．

Answer 1

考点：直线的斜率

专题：直线与圆

分析：由直线系方程求出直线所过定点，再由两点求斜率求得定点与线段两端点连线的斜率，数形结合求得实数k的取值范围．

解答： 解：由直线kx+y+2=0可知直线过定点P（0，-2），
又M（-2，1），N（3，2），如图，

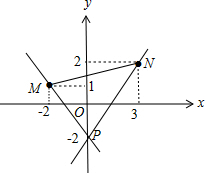
kPM=

-2-1

0-(-2)

=-

3

2

，kPN=

-2-2

0-3

=

4

3

．
∴直线kx+y+2=0和以M（-2，1），N（3，2）为端点的线段相交，
则-k的取值范围为（-∞，-

3

2

]∪[

4

3

，+∞）．
k的取值范围是：（-∞，-

4

3

]∪[

3

2

，+∞）．
故答案为：（-∞，-

4

3

]∪[

3

2

，+∞）．

点评：本题考查了直线系方程的应用，考查了两点求直线的斜率，考查了数形结合的解题思想方法，是中档题．