题目内容

6．用火柴棒摆“金鱼”，如图所示：

按照上面的规律，第5个“金鱼”图需要火柴棒的根数为（　　）
A．28B．32C．40D．42

分析 由图形间的关系可以看出，每多出一个小金鱼，则要多出6根火柴棒，则组成不同个数的图形的火柴棒的个数组成一个首项是8，公差是6的等差数列，写出通项，求出第n项的火柴根数．

解答 解：∵第一个图中有8根火柴棒组成，
第二个图中有8+6个火柴棒组成，
第三个图中有8+2×6个火柴组成，
以此类推
组成n个系列正方形形的火柴棒的根数是8+6（n-1）
∴第5个图中的火柴棒有8+6×4=32
故选：B

点评 本题考查归纳推理，考查等差数列的通项，解题的关键是看清随着小金鱼的增加，火柴的根数的变化趋势，看出规律．

练习册系列答案
相关题目
16．已知直线l的参数方程：$\left\{\begin{array}{l}x=t\\ y=1+2t\end{array}$（t为参数）和圆C的极坐标方程：ρ=4$\sqrt{2}$sin（θ+$\frac{π}{4}$）．P（0，1）
（1）将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
（2）判断直线l和圆C的位置关系，若相交于两点A、B，求|PA|•|PB|．
17．在△ABC中，M是线段AB的中点，$\overrightarrow{AN}=\frac{1}{2}\overrightarrow{NC}$，BN与CM相交于点E，设$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，
（1）用基底$\vec a$，$\vec b$表示$\overrightarrow{BN}$和$\overrightarrow{CM}$；
（2）用基底$\vec a$，$\vec b$表示$\overrightarrow{AE}$．
14．观察下列数表：
2
4，6
8，10，12，14
16，18，20，22，24，26，28，30
…
设2016是该表第m行的第n个数，则m+n=507．
1．网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为（　　）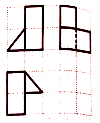
A．2B．4C．$\frac{2\sqrt{2}}{3}$D．1+$\frac{2\sqrt{2}}{3}$
11．某班有30名男生，20名女生，现要从中选出5人组成一个宣传小组，其中男、女学生均不少于2人的选法为（　　）
A．$C_{30}^2$$C_{20}^2$$C_{46}^1$
B．$C_{50}^5-C_{30}^5-C_{20}^5$
C．$C_{50}^5-C_{30}^1C_{20}^4-C_{30}^4C_{20}^1$
D．$C_{30}^3C_{20}^2+C_{30}^2C_{20}^3$
18．在极坐标系中，点$A（3，\frac{5π}{12}）$与点$B（8，\frac{π}{12}）$之间的距离等于7．
15．已知集合A={x|x2-4x-5≤0}，函数y=ln（x2-4）的定义域为B．
（Ⅰ）求A∩B；
（Ⅱ）若C={x|x≤a-1}，且A∪（∁RB）⊆C，求实数a的取值范围．
2．已知等差数列{an}中，a2，a2016是方程x2-2x-2=0的两根，则S2017=（　　）
A．-2017B．-1008C．1008D．2017

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网