题目内容
若实数x，y满足x2+y2-2x+4y=0，求y-2x的最大值．
考点：直线与圆的位置关系
专题：计算题,直线与圆
分析：设z=y-2x，则y=z+2x，代入x2+y2-2x+4y=0，可得5x2+（4z+6）x+4z+z2=0，利用△=（4z+6）2-20（4z+z2）≥0，求出z的范围，从而得到z=x-2y的最大值．
解答：
解：设z=y-2x，则y=z+2x，
代入x2+y2-2x+4y=0，可得5x2+（4z+6）x+4z+z2=0，
∴△=（4z+6）2-20（4z+z2）≥0，
∴z2+8z-9≤0，
∴-9≤z≤1，
故y-2x的最大值为1．
代入x2+y2-2x+4y=0，可得5x2+（4z+6）x+4z+z2=0，
∴△=（4z+6）2-20（4z+z2）≥0，
∴z2+8z-9≤0，
∴-9≤z≤1，
故y-2x的最大值为1．
点评：本题主要考查了简单的转化思想，属中档题．利用△=（4z+6）2-20（4z+z2）≥0是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
设a=sin33°，b=cos55°，c=tan55°，则（ ）
| A、a＞b＞c |
| B、b＞c＞a |
| C、c＞b＞a |
| D、c＞a＞b |
“k＞9”是“
+
=1表示双曲线”的（ ）
| x2 |
| 9-k |
| y2 |
| 4+k |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
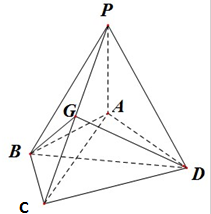如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=BC=2，AD=CD=