题目内容
已知椭圆Γ: (a>b>0)过点A(0,2),离心率为
(a>b>0)过点A(0,2),离心率为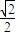 ,过点A的直线l与椭圆交于另一点M.
,过点A的直线l与椭圆交于另一点M.(I)求椭圆Γ的方程;
(II)是否存在直线l,使得以AM为直径的圆C,经过椭圆Γ的右焦点F且与直线 x-2y-2=0相切?若存在,求出直线l的方程;若不存在,请说明理由.
【答案】分析:(Ⅰ)由点A(0,2)可得b值,由离心率为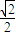 可得
可得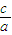 =
= ,再由a2=b2+c2,联立方程组即可求得a,b值;
,再由a2=b2+c2,联立方程组即可求得a,b值;
(II)假设存在直线l,使得以AM为直径的圆C,经过椭圆后的右焦点F且与直线x-2y-2=0相切,根据以AM为直径的圆C过点F可得∠AFM=90°,求出直线MF方程,联立直线MF方程与椭圆方程可得求得M坐标,利用直线与圆相切的条件d=r分情况验证圆与直线x-2y-2=0相切即可;
解答:解:(Ⅰ)依题意得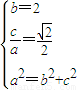 ,解得
,解得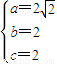 ,
,
所以所求的椭圆方程为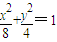 ;
;
(Ⅱ)假设存在直线l,使得以AM为直径的圆C,经过椭圆后的右焦点F且与直线x-2y-2=0相切,
因为以AM为直径的圆C过点F,所以∠AFM=90°,即AF⊥AM,
又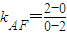 =-1,所以直线MF的方程为y=x-2,
=-1,所以直线MF的方程为y=x-2,
由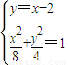 消去y,得3x2-8x=0,解得x=0或x=
消去y,得3x2-8x=0,解得x=0或x= ,
,
所以M(0,-2)或M( ,
, ),
),
(1)当M为(0,-2)时,以AM为直径的圆C为:x2+y2=4,
则圆心C到直线x-2y-2=0的距离为d=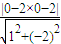 =
=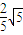 ≠
≠ ,
,
所以圆C与直线x-2y-2=0不相切;
(2)当M为( ,
, )时,以AM为直径的圆心C为(
)时,以AM为直径的圆心C为(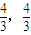 ),半径为r=
),半径为r=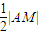 =
=
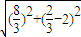 =
= ,
,
所以圆心C到直线x-2y-2=0的距离为d= =r,
=r,
所以圆心C与直线x-2y-2=0相切,此时kAF= ,所以直线l的方程为y=-
,所以直线l的方程为y=-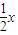 +2,即x+2y-4=0,
+2,即x+2y-4=0,
综上所述,存在满足条件的直线l,其方程为x+2y-4=0.
点评:本题考直线与圆锥曲线的关系、椭圆方程的求解,考查直线与圆的位置关系,考查分类讨论思想,解决探究型问题,往往先假设存在,由此推理,若符合题意,则存在,否则不存在.
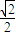 可得
可得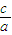 =
= ,再由a2=b2+c2,联立方程组即可求得a,b值;
,再由a2=b2+c2,联立方程组即可求得a,b值;(II)假设存在直线l,使得以AM为直径的圆C,经过椭圆后的右焦点F且与直线x-2y-2=0相切,根据以AM为直径的圆C过点F可得∠AFM=90°,求出直线MF方程,联立直线MF方程与椭圆方程可得求得M坐标,利用直线与圆相切的条件d=r分情况验证圆与直线x-2y-2=0相切即可;
解答:解:(Ⅰ)依题意得
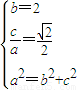 ,解得
,解得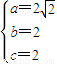 ,
,所以所求的椭圆方程为
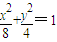 ;
;(Ⅱ)假设存在直线l,使得以AM为直径的圆C,经过椭圆后的右焦点F且与直线x-2y-2=0相切,
因为以AM为直径的圆C过点F,所以∠AFM=90°,即AF⊥AM,
又
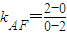 =-1,所以直线MF的方程为y=x-2,
=-1,所以直线MF的方程为y=x-2,由
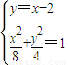 消去y,得3x2-8x=0,解得x=0或x=
消去y,得3x2-8x=0,解得x=0或x= ,
,所以M(0,-2)或M(
 ,
, ),
),(1)当M为(0,-2)时,以AM为直径的圆C为:x2+y2=4,
则圆心C到直线x-2y-2=0的距离为d=
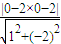 =
=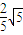 ≠
≠ ,
,所以圆C与直线x-2y-2=0不相切;
(2)当M为(
 ,
, )时,以AM为直径的圆心C为(
)时,以AM为直径的圆心C为(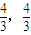 ),半径为r=
),半径为r=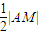 =
=
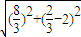 =
= ,
,所以圆心C到直线x-2y-2=0的距离为d=
 =r,
=r,所以圆心C与直线x-2y-2=0相切,此时kAF=
 ,所以直线l的方程为y=-
,所以直线l的方程为y=-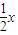 +2,即x+2y-4=0,
+2,即x+2y-4=0,综上所述,存在满足条件的直线l,其方程为x+2y-4=0.
点评:本题考直线与圆锥曲线的关系、椭圆方程的求解,考查直线与圆的位置关系,考查分类讨论思想,解决探究型问题,往往先假设存在,由此推理,若符合题意,则存在,否则不存在.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
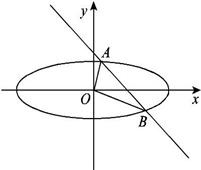 已知椭圆
已知椭圆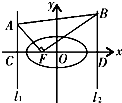 如图,已知椭圆
如图,已知椭圆