题目内容
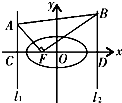 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
分析:如图所示,作法线FM交AB于点M,利用光线的反射性质及∠AFB=90°,可得∠AFB=∠BFM=45°.进而得到∠AFC=45°=∠BFD.于是得到Rt△ACF与Rt△BFD分别是等腰直角三角形.由于∠CAB=105°,可得∠BAF=60°.又|AF|=
|CF|,|BF|=
|FD|,及|BF|=
|AF|.即可得出椭圆的离心率.
| 2 |
| 2 |
| 3 |
解答:解:如图所示,
作法线FM交AB于点M,∵∠AFB=90°,∴∠AFB=∠BFM=45°.
∴∠AFC=45°,∠BFD=45°.
∴Rt△ACF与Rt△BFD分别是等腰直角三角形.
∴|AF|=
|CF|=
(
-c),|BF|=
|FD|=
|
+c|.
∵∠CAB=105°,∴∠BAF=105°-45°=60°.
∴|BF|=
|AF|.
∴
|
+c|=
•
|
-c|,
化为(
-1)a2=(
+1)c2,解得
=
.
故选:A.

作法线FM交AB于点M,∵∠AFB=90°,∴∠AFB=∠BFM=45°.
∴∠AFC=45°,∠BFD=45°.
∴Rt△ACF与Rt△BFD分别是等腰直角三角形.
∴|AF|=
| 2 |
| 2 |
| a2 |
| c |
| 2 |
| 2 |
| a2 |
| c |
∵∠CAB=105°,∴∠BAF=105°-45°=60°.
∴|BF|=
| 3 |
∴
| 2 |
| a2 |
| c |
| 3 |
| 2 |
| a2 |
| c |
化为(
| 3 |
| 3 |
| c |
| a |
| ||||
| 2 |
故选:A.
点评:本题考查了椭圆的标准方程及其性质、光线的反射性质、等腰直角三角形及含60°角的直角三角形的性质等基础知识与基本技能方法,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
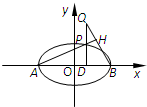 如图,已知椭圆
如图,已知椭圆 (2013•汕头一模)如图.已知椭圆
(2013•汕头一模)如图.已知椭圆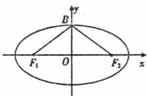 (2012•安徽模拟)如图,已知椭圆
(2012•安徽模拟)如图,已知椭圆 (2011•崇明县二模)如图,已知椭圆
(2011•崇明县二模)如图,已知椭圆 如图,已知椭圆
如图,已知椭圆