Question

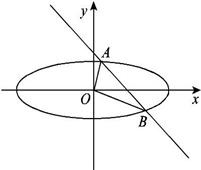已知椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)，与直线x+y-1=0相交于A，B两点，且OA⊥OB，为坐标原点．
（Ⅰ）求

1

a2

+

1

b2

的值；
（Ⅱ）若椭圆长轴长的取值范围是[

5

，

6

]，求椭圆离心率的取值范围．

Answer 1

分析：本题主要考查椭圆的标准方程与性质、直线与椭圆的位置关系及参数的求值问题，
（Ⅰ）通过直线与椭圆的位置关系，利用代入法求解相应的代数式的值；
（Ⅱ）利用长轴长的取值范围，结合关系式与不等式的求解来确定离心率的取值范围．

解答：解：（Ⅰ）将x+y-1=0代入椭圆方程整理得（a²+b²）x²-2a²x+a²（1-b²）=0（﹡）
设A（x₁，y₁），B（x₂，y₂），
则x1+x2=

2a2

a2+b2

，x1x2=

a2(1-b2)

a2+b2

，
而y1y2=(1-x1)(1-x2)=

b2(1-a2)

a2+b2

．（3分）
又∵OA⊥OB，∴x₁x₂+y₁y₂=0∴

a2(1-b2)

a2+b2

+

b2(1-a2)

a2+b2

=0∴a²+b²=2a²b²，∴

1

a2

+

1

b2

=2①
经验证，此时方程（﹡）有解，∴

1

a2

+

1

b2

=2（7分）
（Ⅱ）将b2=a2-c2，e=

c

a

代入①得
2-e²=2a²（1-e²），∴e2=

2a2-2

2a2-1

=1-

1

2a2-1

（10分）
而2a∈[

5

，

6

]，∴

1

3

≤e2≤

1

2

而0＜e＜1，∴

3

3

≤e≤

2

2

故e的取值范围为[

3

3

，

2

2

]（13分）．

点评：本题是直线与圆锥曲线的综合问题．近年高考中圆锥曲线问题的解答难度有逐渐变低的趋势．通过解析几何自身的特点，结合相应的数学知识，比如不等式、数列、函数、向量、导数等，考查各知识点之间的综合应用，也是考查学生综合能力的一大考点．在新课标的高考中，圆锥曲线的考查以基础知识为主，难度不会太大．