题目内容
 如图,在边长为2正方形ABCD内作内切圆O,则将圆O绕对角线AC旋转一周得到的旋转体的表面积为( )
如图,在边长为2正方形ABCD内作内切圆O,则将圆O绕对角线AC旋转一周得到的旋转体的表面积为( )A、
| ||
| B、4 | ||
C、
| ||
| D、4π |
考点:旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离
分析:根据球的体积公式和圆锥的体积公式,分别求出V1,V2,可得答案.
解答:
解:∵正方形ABCD的边长为2,
故AC=BD=2
,
则正方形ABCD旋转后得到两个底面半径为
,高为
的圆锥形成的组合体,
故V1=2×
×π×
2×
=
,
圆O绕对角线AC旋转一周得到一个半径为1的球,
故V2=
=
,
故V1:V2=
:1,
故选:D
故AC=BD=2
| 2 |
则正方形ABCD旋转后得到两个底面半径为
| 2 |
| 2 |
故V1=2×
| 1 |
| 3 |
| 2 |
| 2 |
4
| ||
| 3 |
圆O绕对角线AC旋转一周得到一个半径为1的球,
故V2=
| 4π |
| 3 |
| 4π |
| 3 |
故V1:V2=
| 2 |
故选:D
点评:本题考查的知识点是旋转体,熟练掌握圆锥和球的体积公式,是解答的关键.

练习册系列答案
相关题目
母线长为1的圆锥的侧面展开图的圆心角为π,则这个圆锥的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
圆锥的表面积公式( )
| A、S=πr2+πrl |
| B、S=2πr2+2πrl |
| C、S=πrl |
| D、S=πr2+πR2+πrl+πRl |
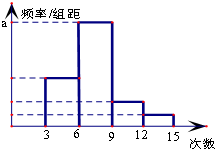 对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对某校高二年级学生参加社区服务次数进行统计,随机抽取N名学生作为样本,得到这N名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: