题目内容
4.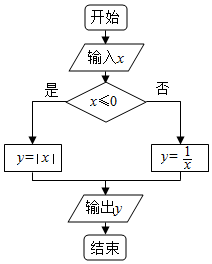 如图给出了一个程序框图,其作用是输入实数x的值,输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值有( )
如图给出了一个程序框图,其作用是输入实数x的值,输出相应的y值,若要使输入的x值与输出的y值相等,则这样的x值有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 无数个 |
分析 由已知的程序框图,我们可得该程序的功能是计算并输出分段函数y=$\left\{\begin{array}{l}{|x|}&{x≤0}\\{\frac{1}{x}}&{x>0}\end{array}\right.$的值,结合输入的x值与输出的y值相等,我们分类讨论后,即可得到结论.
解答 解:由题意得该程序的功能是:
计算并输出分段函数y=$\left\{\begin{array}{l}{|x|}&{x≤0}\\{\frac{1}{x}}&{x>0}\end{array}\right.$的值,
又∵输入的x值与输出的y值相等,
当x≤0时,x=|x|,解得x=0,
当x>0时,x=$\frac{1}{x}$,解得x=1或-1(舍去).
故满足条件的x值共有2个.
故选:B.
点评 本题考查的知识点是选择结构,其中分析出函数的功能,将问题转化为分段函数函数值问题,是解答本题的关键.

练习册系列答案
相关题目
17.椭圆4x2+y2=k上任意两点的最大距离为8,则k的值为( )
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
15.sin20°cos10°+cos20°sin10°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\frac{1}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
9.执行如图的程序框图,则输出的s=( )


| A. | $\frac{1}{16}$ | B. | -$\frac{1}{16}$ | C. | $\frac{1}{32}$ | D. | -$\frac{1}{32}$ |
14.已知f(x)=(4-m)x2-4x+1,a为正整数,满足f(a)<0的a的个数有且仅有两个,则实数m的取值范围为( )
| A. | 2<m≤3 | B. | $\frac{9}{4}<m≤\frac{25}{9}$ | C. | m$>\frac{25}{9}$ | D. | m$≤\frac{9}{4}$ |