题目内容
17．椭圆4x2+y2=k上任意两点的最大距离为8，则k的值为（ ）| A． | 4 | B． | 8 | C． | 16 | D． | 32 |
分析 将椭圆方程化为标准方程，可得椭圆上两点的距离的最大值为2a，解方程即可得到k．
解答 解：椭圆4x2+y2=k的标准方程为$\frac{{x}^{2}}{\frac{k}{4}}$+$\frac{{y}^{2}}{k}$=1，
由k＞$\frac{k}{4}$，可得椭圆上任意两点的距离的最大值为2a=2$\sqrt{k}$=8，
解得k=16．
故选：C．
点评 本题考查椭圆的方程和性质，注意运用椭圆的标准方程，考查运算能力，属于基础题．
练习册系列答案
相关题目
7．已知椭圆：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左顶点为A，上顶点为B，右焦点为F，过A、B、F作圆C，若圆心C的横纵坐标相等，则该椭圆的离心率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
12．已知x，y都是正数，且x+y=1，则$\frac{4}{x+2}$+$\frac{1}{y+1}$的最小值为（ ）
| A． | $\frac{13}{15}$ | B． | 2 | C． | $\frac{9}{4}$ | D． | 3 |
9．x＞2是x＞4的（ ）
| A． | 充分条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 即非充分又非必要条件 |
3．双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）左右焦点分别为F1、F2，以F1F2为边作正三角形，与双曲线在第一二象限的交点恰是所在边中点，则双曲线的离心率为（ ）
| A． | 2$\sqrt{3}+1$ | B． | $\sqrt{3}$ | C． | $\sqrt{3}+1$ | D． | 2$\sqrt{3}$ |
4．
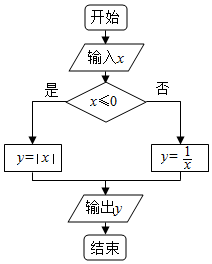如图给出了一个程序框图，其作用是输入实数x的值，输出相应的y值，若要使输入的x值与输出的y值相等，则这样的x值有（ ）
如图给出了一个程序框图，其作用是输入实数x的值，输出相应的y值，若要使输入的x值与输出的y值相等，则这样的x值有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 无数个 |