题目内容
已知集合A={x|y=
}，B={y|y=a-2x-x2}，其中a∈R，如果A⊆B，求实数a的取值范围．
| 3-|x| |
考点：集合的包含关系判断及应用
专题：计算题,集合
分析：由题设条件，可先化简两个集合，再由两个集合的包含关系得出参数的取值范围即可
解答：
解：对于集合A：令3-|x|≥0，解得-3≤x≤3，即A={x|-3≤x≤3}，
对于集合B：y=a-2x-x2=a+1-（x+1）2≤a+1，即B═{y|y≤a+1}，
∵a∈R，A⊆B
∴a+1≥3，解得a≥2
综上，实数a的取值范围a≥2
对于集合B：y=a-2x-x2=a+1-（x+1）2≤a+1，即B═{y|y≤a+1}，
∵a∈R，A⊆B
∴a+1≥3，解得a≥2
综上，实数a的取值范围a≥2
点评：本题考查集合的包含关系及应用，解答的关键是化简两个集合及熟练利用集合的包含关系转化
练习册系列答案
应用题作业本系列答案
相关题目
已知f（x）为R上的可导函数，且满足f（x）＞f′（x），对任意正实数a，下面不等式恒成立的是（ ）
A、f(a)＞
| ||
B、f(a)＜
| ||
| C、f（a）＞eaf（0） | ||
| D、f（a）＜eaf（0） |
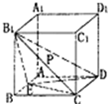如图，正方体ABCD-A1B1C1D1的棱长为1，E是AB的中点，P是B1C的中点．
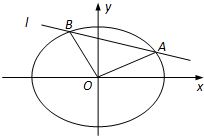在平面直角坐标系xOy中，设椭圆C的中心在原点，焦点在x轴上，短半轴长为2，椭圆C长轴的右端点到其右焦点的距离为
进入2013年后全国各地雾霾天气频发，一个重要的诱因是空气中细小颗粒物．我国新引入PM2.5来衡量大气的质量．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．我国PM2.5标准采用世卫组织设定的最宽限值，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米～75微克/立方米之间空气质量为二级；在75微克/立方米及其以上空气质量为超标．长沙市环保局从该市市区2013年1月份的PM2.5监测数据中随机抽取7天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）．
如图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图．从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是双曲线y2-
=1的离心率e=2，则以双曲线的两条渐近线与抛物线y2=mx的交点为顶点的三角形的面积为（ ）
| x2 |
| m |
A、
| ||
B、9
| ||
C、27
| ||
D、36
|