题目内容
下列命题中的假命题是( )
| A、?x∈R,2x-1>0 |
| B、?x∈R,lgx<1 |
| C、?x∈N+,(x-1)2>0 |
| D、?x∈R,tanx=2 |
考点:命题的真假判断与应用,函数的单调性及单调区间
专题:简易逻辑
分析:A.利用指数函数的单调性即可得出;
B.利用对数函数的单调性即可得出;
C.取x=1即可判断出;
D.利用正切函数的单调性即可得出.
B.利用对数函数的单调性即可得出;
C.取x=1即可判断出;
D.利用正切函数的单调性即可得出.
解答:
解:A.?x∈R,2x-1=
>0正确;
B.当0<x<10时,lgx<1正确;
C.当x=1,(x-1)2=0,因此不正确;
D.存在x∈R,tanx=2成立,正确.
综上可知:只有C错误.
故选:C.
| 2x |
| 2 |
B.当0<x<10时,lgx<1正确;
C.当x=1,(x-1)2=0,因此不正确;
D.存在x∈R,tanx=2成立,正确.
综上可知:只有C错误.
故选:C.
点评:本题考查了指数函数与对数函数、正切函数的单调性,属于基础题.

练习册系列答案
相关题目
下列说法中错误的是( )
| A、对于命题p:x0∈R,sin x0>1,则¬p:x∈R,sin x≤1 |
| B、命题“若0<a<1,则函数f(x)=ax在R上是增函数”的逆命题为假命题 |
| C、若p∨q为真命题,则p,q均为真命题 |
| D、命题“若x2-x-2=0,则x=2”的逆否命题是“若x≠2,则x2-x-2≠0” |
双曲线y2-
=1的离心率e=2,则以双曲线的两条渐近线与抛物线y2=mx的交点为顶点的三角形的面积为( )
| x2 |
| m |
A、
| ||
B、9
| ||
C、27
| ||
D、36
|
执行如图所示的程序框图.若输入x=7,则输出k的值是( )


| A、2 | B、3 | C、4 | D、5 |
下列说法正确的是( )
| A、?x0∈R,ex0≤0 | ||
| B、对?a>b,则ab=2,(a2+b2)min=4 | ||
| C、a>1,b>1是ab>1的充分条件 | ||
D、a+b=0的充要条件是
|
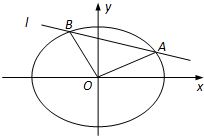 在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C长轴的右端点到其右焦点的距离为
在平面直角坐标系xOy中,设椭圆C的中心在原点,焦点在x轴上,短半轴长为2,椭圆C长轴的右端点到其右焦点的距离为