题目内容
1.函数y=$\sqrt{x}$+$\sqrt{2-x}$的最大值为2.分析 由$\frac{{a}^{2}+{b}^{2}}{2}$≥($\frac{a+b}{2}$)2,即有a+b≤$\sqrt{2({a}^{2}+{b}^{2})}$,即可得到所求函数的最大值.
解答 解:当a≥0,b≥0,$\frac{{a}^{2}+{b}^{2}}{2}$-($\frac{a+b}{2}$)2=$\frac{2{a}^{2}+2{b}^{2}-{a}^{2}-{b}^{2}-2ab}{4}$
=$\frac{(a-b)^{2}}{4}$≥0,
可得$\frac{{a}^{2}+{b}^{2}}{2}$≥($\frac{a+b}{2}$)2,即有a+b≤$\sqrt{2({a}^{2}+{b}^{2})}$,
当且仅当a=b时,取得等号.
则有y=$\sqrt{x}$+$\sqrt{2-x}$≤$\sqrt{2(x+2-x)}$=2,
当且仅当x=1时,取得最大值2.
故答案为:2.
点评 本题考查函数的最值的求法,注意运用重要不等式$\frac{{a}^{2}+{b}^{2}}{2}$≥($\frac{a+b}{2}$)2,考查运算能力,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
9.函数f(x)=x3-$\frac{1}{x}$的图象关于( )
| A. | y轴对称 | B. | 直线y=-x对称 | C. | 坐标原点对称 | D. | 直线y=x对称 |
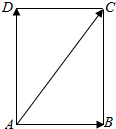 一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.
一艘货船从A点出发,以v km/h的速度向垂直于岸边DC的方向行驶,同时河水的流速为2km/h,河水流动的方向为$\overrightarrow{AB}$,货船实际航行的方向为$\overrightarrow{AC}$,而且$\overrightarrow{AC}$与$\overrightarrow{AB}$的夹角为$\frac{π}{3}$,求v.