题目内容
7.在△ABC中,角A,B,C的对边分别为a,b,c,且acosB+bcosA=2ccosC.(Ⅰ)求角C;
(Ⅱ)若c=2$\sqrt{3}$,求△ABC面积的最大值.
分析 (Ⅰ)由题意和正余弦定理及和差角的三角函数公式,易得cosC,由三角形内角的范围可得.
(Ⅱ)利用余弦定理、基本不等式的性质、三角形面积计算公式即可得出.
解答 (本题满分为12分)
解:(Ⅰ)∵在△ABC中acosB+bcosA=2ccosC,
∴由正弦定理可得sinAcosB+sinBcosA=2sinCcosC,
∴sin(A+B)=2sinCcosC,
∴sinC=2sinCcosC,
∴解得:cosC=$\frac{1}{2}$,
∴由三角形内角的范围可得角C=$\frac{π}{3}$.
(Ⅱ)由余弦定理可得:12=c2=a2+b2-2abcosC≥2ab-ab=ab,
可得ab≤12,当且仅当a=2$\sqrt{3}$时取等号.
∴△ABC面积的最大值=$\frac{1}{2}×12×sin\frac{π}{3}$=3$\sqrt{3}$.
点评 本题考查了正弦定理余弦定理、三角形面积计算公式、和差公式、基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
17.已知椭圆C:$\frac{{x}^{2}}{2}$+y2=1,若一组斜率为$\frac{1}{4}$的平行直线被椭圆C所截线段的中点均在直线l上,则l的斜率为( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
18.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$,其中|$\overrightarrow{a}$|=$\sqrt{2}$,|$\overrightarrow{b}$|=2,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{a}$,则向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角是( )
| A. | $\frac{3π}{4}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
15.已知Sn是等差数列an的前n项和,且S3=2a1,则下列结论错误的是( )
| A. | a4=0 | B. | S4=S3 | C. | S7=0 | D. | an是递减数列 |
12.已知集合A={x|-1<x<2},$B=\left\{{x|y={x^{-\frac{1}{2}}}}\right\}$,则A∩B=( )
| A. | (0,+∞) | B. | (-1,2) | C. | (0,2) | D. | (2,+∞) |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.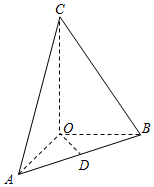 在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.
在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.